Perpendicular Bisector Calculator

The bisector can either cross the line segment it bisects, or can be a line segment or ray that ends at the line.

Perpendicular line equation calculator used to find the equation of perpendicular bisector. It is also known as angle bisector.

What is perpendicular? What is a perpendicular bisector? How to find a perpendicular line? These are the questions we are going to answer in this space.

Perpendicular bisector definition

Perpendicular Bisector is the division of something into two equal or congruent parts. It is a line, ray, or segment which cuts another line segment into two equal parts at 90 degrees.

The perpendicular bisector equation can be effortlessly calculated using the perpendicular bisector calculator. Constructing a perpendicular bisector could be convenient if you know how to use a compass?

Perpendicular Bisector of a line segment

If a line is perpendicular to another line and dividing into two equal parts, it will be a perpendicular bisector of a line segment. See the figure below:

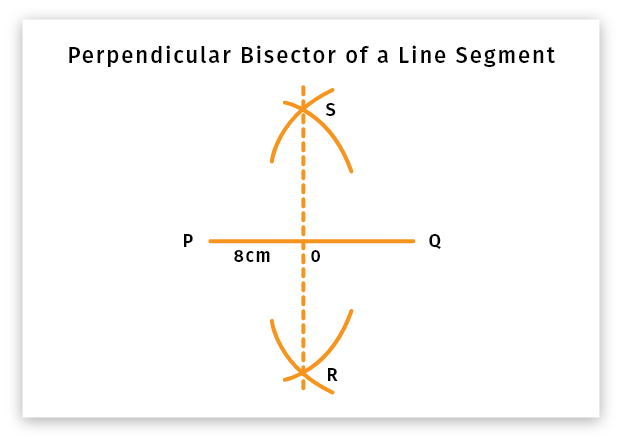
Use the perpendicular line calculator to calculate the perpendicular bisector equation.

Perpendicular Bisector of a Triangle

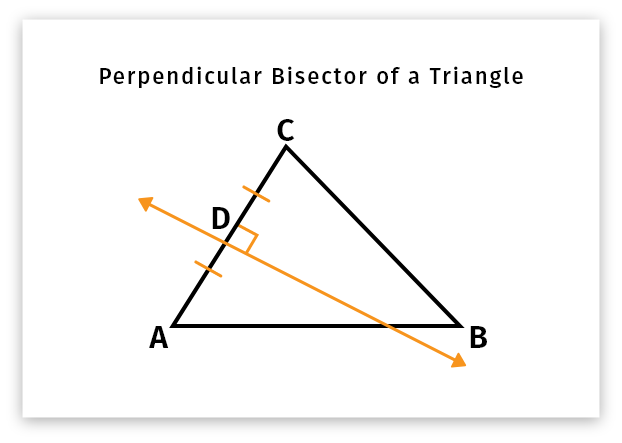
If a line is perpendicular to the side of a triangle and crossing it through the midpoint, it will be the perpendicular bisector of a triangle.

Perpendicular Bisector of a Circle

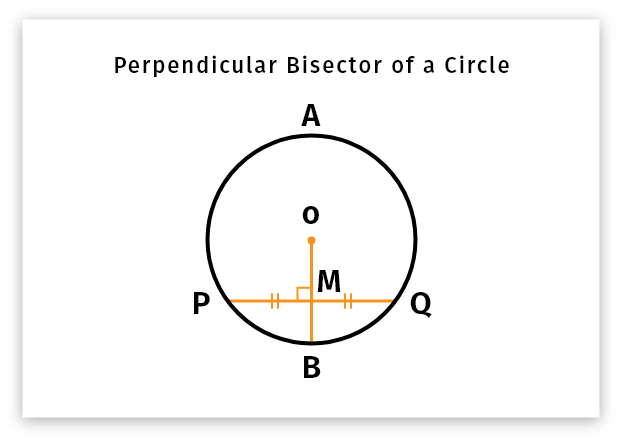
If a line is perpendicular to a chord of a circle and passes through the midpoint of that circle, it will be the perpendicular bisector of a circle.

Perpendicular Bisector of a Rhombus

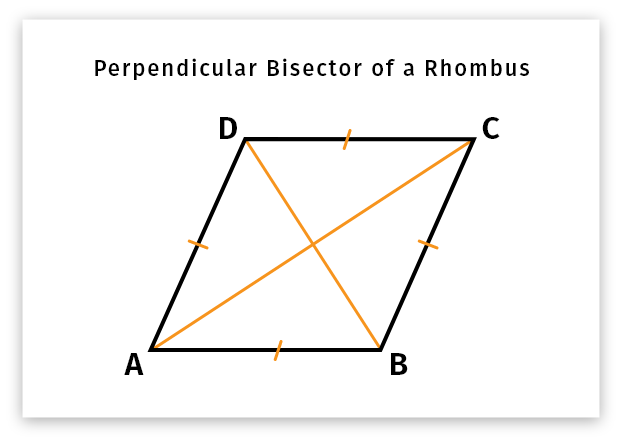
The diagonals of a rhombus are the perpendicular bisector of the rhombus as those diagonals are always perpendicular to each other dividing the sides of the rhombus into two equal parts.

How to find perpendicular bisector?

Example:
Let's find the perpendicular bisector equation with points P(3,4) and Q(6,6).

Solution

Consider the coordinates of the points P and Q to be x1,y1, and x2,y2 respectively. We need to calculate the midpoints of the line PQ, which is F, and the slope to find the equation of the perpendicular bisector.

Step 1:
Let's calculate the midpoint of the line which is the average of the x and y coordinates.

Midpoint of a line = x1+x2/2, y1+y2/2

Midpoint of PQ = 3+6/2, 4+6/2 = (9/2, 10/2)

Step 2:
Next, we need to find the slope of the line PQ using the formula y2-y1/x2-x1. Kindly note that the slope is represented by the letter 'm'.

Slope of PQ (m) = 6-7/6-5 = -1 =  6-4 /6-3 = 2/3 = 0.4

Step 3:
Now, let's calculate the slope of the perpendicular bisector (AB) of the line PQ. The slope of the perpendicular bisector = -1/slope of the line.

Therefore for AB = -1/0.4   = -2.5

Step 4:
Once we find the slope as above, we can find the equation with the slope and the midpoints.

Lets find the equation of the AB with midpoints (9/2,10/2) and the slope -2.5.

Formula to find the equation: y-y1 = m(x-x1) y-10/2 = -2.5(x-9/2)

By solving the above, we get the equation y-5 = -2.5 (x-9/2).

This is the perpendicular bisector equation (AB) of the line PQ.compound interest allows your money to earn even more money over time.