Point Slope Form Calculator

Point slope form calculator

Point slope form calculator is an online tool to find the general equation of a line as (y - y₁ = m(x - x₁). The Point slope calculator is an intuitive tool that lets you calculate the slope and straight-line equation in no time.

What is the point-slope form?

The point-slope form is defined as the difference in the y-coordinate between two points (y - y₁) on a line that is proportional to the difference in the x-coordinate points (x - x₁). The point-slope form is about having a single point and a direction and converting that between an algebraic equation and a graph.

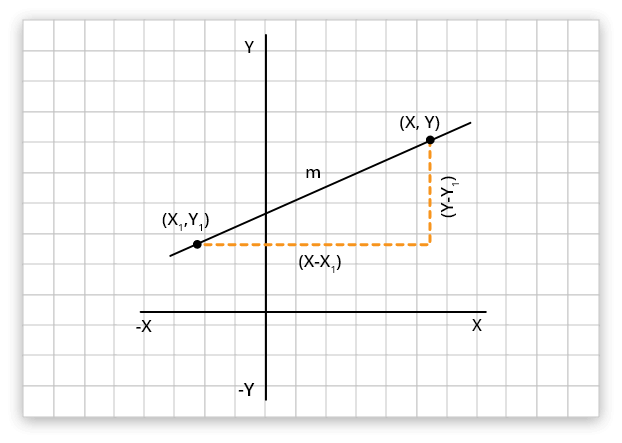
It can also be stated as:  

“The equation of a straight line in the form y − y₁ = m(x − x₁) where m is the slope of the line and (x₁, y₁) are the coordinates of a given point on the line.” 

Point slope formula

The point slope formula can be expressed as:

y - y₁ = m(x- x₁)

Where:

• m refers to the slope of the line
• x represents the coordinate on the x-axis
• y represents the coordinate on the y-axis.  

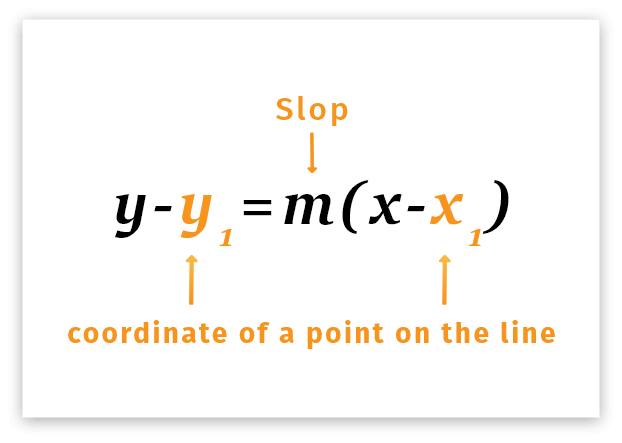
The point-slope form is about having a single point and a direction and converting that between an algebraic equation and a graph. We can derive the slope of a line formula from the above point slope form equation.

m = (y - y₁) / (x- x₁)

How to find point slope form?

The point-slope form can be calculated using the above point slope formula calculator. On the other hand, it can also be calculated using the formula for the point slope form stated above. To find the point slope form manually, follow the steps below:

• Write down the coordinates for x₁, y_1, and slope
• Write down the point-slope formula.
• Substitute the values in the formula and calculate the equation of a line.

Point Slope Form Examples:

Example 1:

Find the equation of the line that passes through (-3, 1) with a slope of 2.

Solution:

Step 1: Write down the coordinates for x₁, y_1, and slope m.

x₁ = -3,
y₁ = 1, and
slope m = 2

Step 2: Write down the point-slope formula and apply that formula.

y - y₁ = m(x- x₁)

Step 3: Substitute the values in the formula and calculate the equation of a line.

y - 1 =2(x - (-3))
y - 1 = 2(x + 3)
y - 1 = 2x + 6

Therefore the Equation = 2x + 6 – y + 1

Equation of the line = 2x – y + 7

Example 2

How do you find the point slope form of points (2, 5) and slope -3?

Solution

Step 1: Write down the coordinates for x₁, y_1, and slope m.

x₁ = 2,
y₁ = 5, and
slope m = -3

Step 2: Write down the point-slope formula and apply that formula.

y - y₁ = m(x- x₁)

Step 3: Substitute the values in the formula and calculate the equation of a line.

y - 5 =-3(x - (2))
y - 5 = -3(x - 2)
y - 5 = -3x + 6
= 3x + y – 5 + 6

Equation of the line = -3x - y + 11

Example 3:

Find the equation of the line that passes through (-3, 1) with a slope of 2.
x₁ = -3,
y₁ = 1 and
slope m = 2.

Apply Formula:
y - y₁ = m(x- x₁)
y-1 =2(x-(-3))
y-1 = 2(x+3)
y-1 = 2x+6

Therefore the Equation = 2x+6-y+1

Equation of the line = 2x-y+7