Dot Product Calculator

Dot Product Calcualtor 

The dot product calculator finds the scalar product of 2-dimensional and 3-dimensional vectors. Users can find the step-by-step process in the result section by clicking on “show more”.

What is dot product?

The dot product of two vectors is also known as its scalar product. This is because the result of this product is always a scalar quantity. It uses the sine function. 

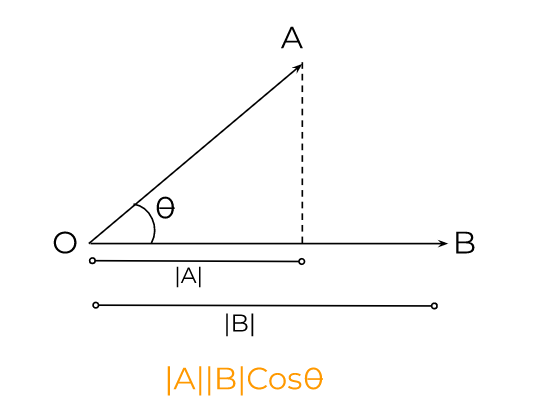
The dot product is helpful in finding the projection of one vector on the other. The dot product abides by the commutative and distributive properties. It is written as A.B and read as A dot B.

Dot product formula: 

Mathematically dot product is written as:

A.B = |A||B| Cosθ

|A| and |B| are the magnitudes of the vectors where theta is the angle between the vectors. 

Another formula is:

A.B = (a₁b₁) + (a₂b₂) + (a₃b₃) + … + (a_nb_n)

How to find the dot product of two vectors?

Unlike the cross product, the dot product only has magnitude and no direction. The steps to calculate dot product by hand are:

1. Find the magnitude of the vector A.
2. Similarly, find the magnitude of the vector B.
3. Calculate the sin of angle using the trigonometry calculator or table. 
4. Put the values in the formula and solve.

The second method is easy, simply multiply the first entry vector A with the first entry of vector B, the second entry of vector A with the second henry of vector B, and so on. Lastly, add all the values.

Example:

What is the value of the dot product for these two vectors?

A = 4 i + 6 j + 5 k
B = 3 i + 2 j + 7 k

Solution:

Step 1: Identify the entries.

a₁ = 4, a₂ = 6, a₃ = 5
b₁ = 3, b₂ = 2, b₃ = 7

Step 2: Put in the formula.

A.B = (a₁b₁) + (a₂b₂) + (a₃b₃) + … + (a_nb_n)
A.B = (4)(3) + (6)(2) + (5)(7) 

Step 3: Solve.

A.B = (4)(3) + (6)(2) + (5)(7) 
A.B = 12 + 12 + 35
A.B = 59