Eigenvalues Calculator

 

Eigenvalues calculator 

Find the possible eigenvalues and eigenvectors for the 2x2, 3x3 to 6x6 matrix using this calculator. See the steps and the whole calculation method involved in finding these values.

Continue reading to see what eigenvalues are and how to calculate them. It is important to have a clear concept of transformation, especially matrix transformation.

What is transformation?

A function applied on ℝⁿ where n is greater than 1 is called transformation. Or to put it simply, a function that deals with 2,3 or more dimensions instead of real numbers, that exist in a one-dimensional plane, is called transformation.

Basically, “the functions involving vectors”. An example of both function and transformation is:

  
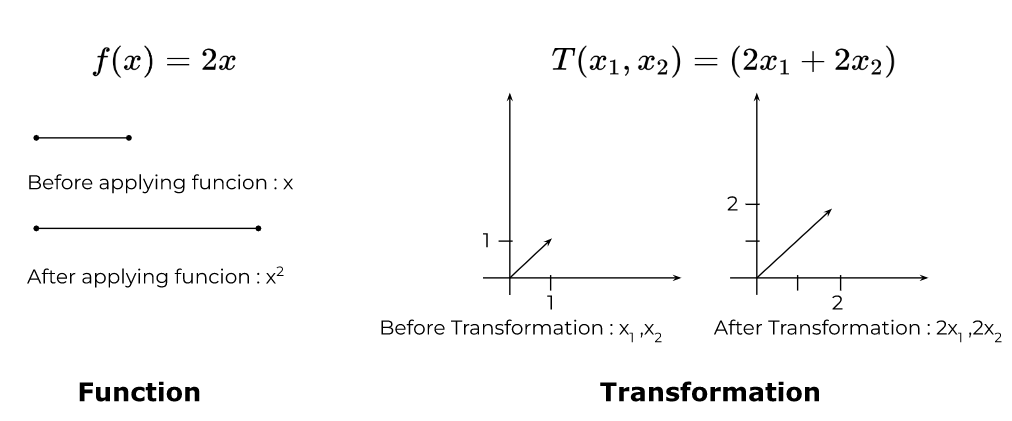
The word “transformation” has more to do with the visual representation of applying the function. It is assumed that a vector moves from one place to another instead of becoming a new vector. 

What are eigenvectors and eigenvalues?

Eigenvector:

During transformation, a vector that changes its direction or magnitude “along the span” of the vector is called an eigenvector.

Usually, we deal with arbitrary values like x or y and it can be any real number. This is why, when you apply a function on an arbitrary vector, all of the real vectors that fit into that arbitrary vector move.

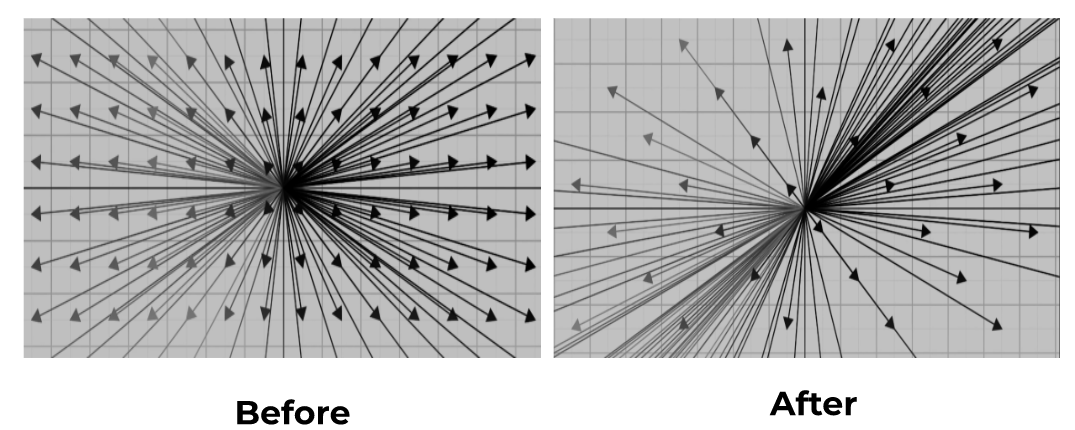
So during transformation, the whole cartesian plane kind of disorientates but its origin remains the same. 

The span of a vector is the line it exists on. It passes through its origin and tip. For an eigenvector, it is necessary for it to stay on its span during transformation. 

For a particular transformation, there are a fixed number of eigenvectors. Its number depends on the matrix that is made by the changes in the basis vectors like i,  j, or k. For example, a 2 by 2 matrix will have a maximum of 2 eigenvectors (actually spaces). 

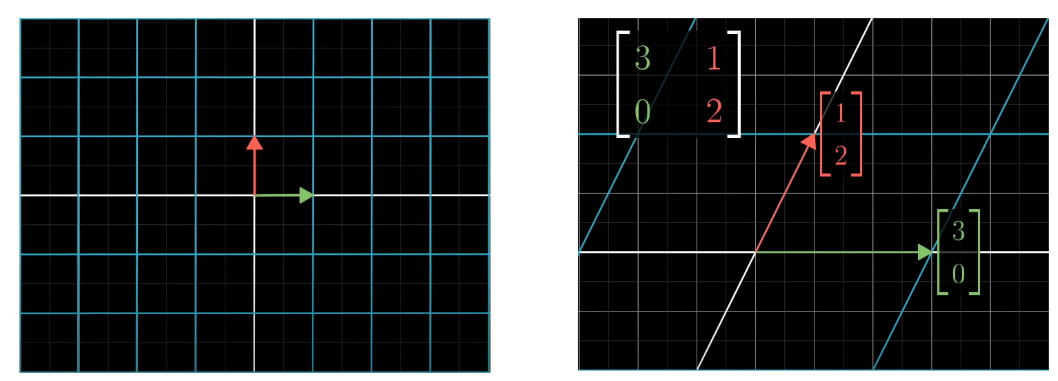
In this image, notice that the i and j moved by some magnitude, and that change when put into a matrix, gives a transformation matrix. One of the two eigenvectors for this particular transformation is (1,-1):

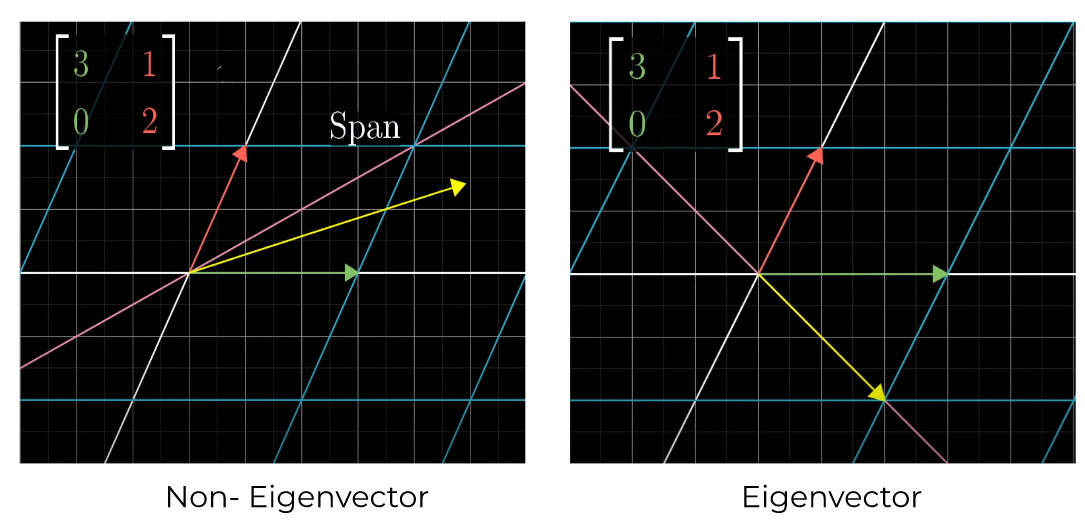
The yellow line is the vector and the pink line shows the span. It can be seen that the eigenvector stayed on its span during transformation. The other eigenvector is the x-axis because it only stretches on its span.

Eigenvalues:

The number by which the vectors get squashed or stretched during transformation. For the above example, the x-axis eigenvector has an eigenvalue of 3. 

Originally, it had a magnitude of 1 but after transformation, it was stretched out 3 times. The second eigenvector has an eigenvalue of 2. 

Eigenvalues can be negative and fractions. It is usually possible to guess eigenvalues by looking at the visual representation but there is still a formula to calculate these.

Eigenvectors make good basis vectors. They are used in 3d rotation, video game development e.t.c

How to find eigenvectors and eigenvalues?

The formula to find eigenvectors and values is derived from the symbolic representation of the eigenvectors. 

Av = λv

• A is the transformation matrix
• v is the eigenvector
• Lambda λ is the scalar number or eigenvalue

This equation means if you multiply the transformation matrix with the eigenvector it will give the same output as the lambda multiplied by the eigenvector. 

It can be proved with an actual example but that would be too long for now. Let’s derive a formula to find the eigenvalues.

The left-hand side is a scalar vector multiplication. To make it similar to the right-hand side, multiply it with an identity matrix.   

Av = λIv

Since the product of scalar and matrix is a matrix, we have matrix-vector multiplication at both sides. Rearranging 

Av - λIv = 0
(A - λI)v = 0 

(A - λI) is a matrix. This will be true for the null vector but that is obvious. You have to figure out non-zero vectors. The eigenvectors will be the members of the null space of this matrix. 

One way to get this product zero is by squishing the matrix into lower dimensions. This is done mathematically by inputting such a value of lambda that makes the determinant of the matrix zero. 

So, the formula for eigenvalues is 

det(A - λI) = 0

Eigenvectors are calculated using eigenvalues. Place the value of lambda in the matrix and replace v and 0 with the matrix-vector form. After that reduce the matrix using reduced row echelon form. 

Further simplification will give the eigenvectors. 

Note: It is possible for a matrix to have one or no eigenvalues.

Eigenspaces:

A set of vectors that satisfy the eigenequation are called eigenspace. They all correspond to the same eigenvalue. Since the eigenvectors exist in the null space of the matrix, so does the eigenspace.

Let’s see an actual example. 

Example: 

For the following matrix, find the eigenvalues and eigenvectors. 

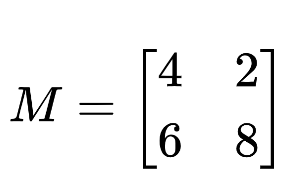
Solution:

Finding eigenvalues:

Step 1: Put the matrix in the formula.

det(A - λI) = 0

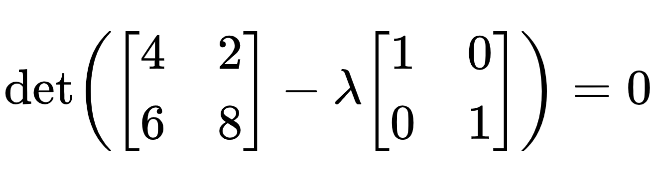
Step 2: Multiply the lambda and subtract with the matrix A.

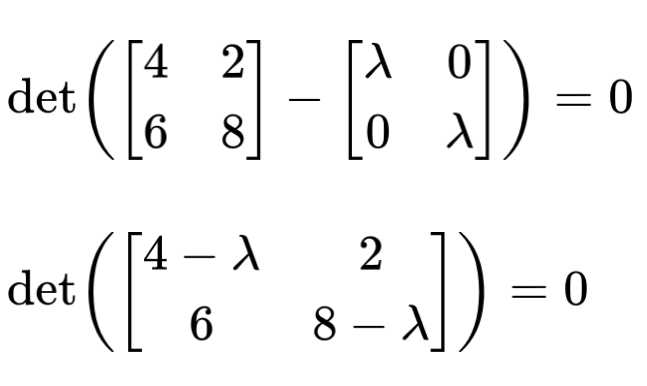
Step 3: Take the determinant.

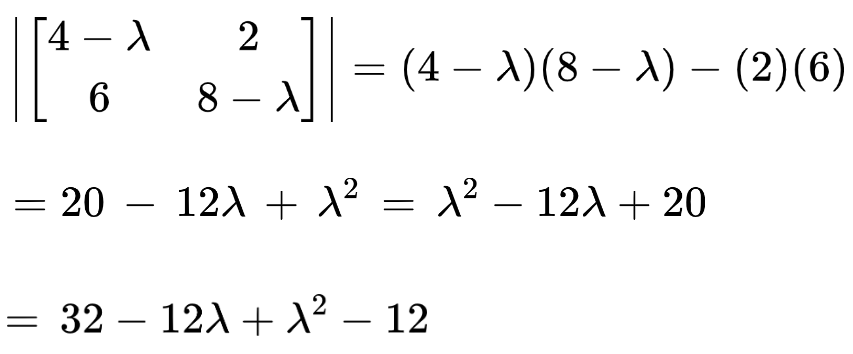
Step 4: Break down into roots using the Quadratic formula calculator.

The two roots are λ = 10 and λ = 2. And these two are the eigenvalues for the given matrix.

Finding the eigenvectors:

Step 1: Put the first value of lambda in the matrix.

(A - λI)v = 0 

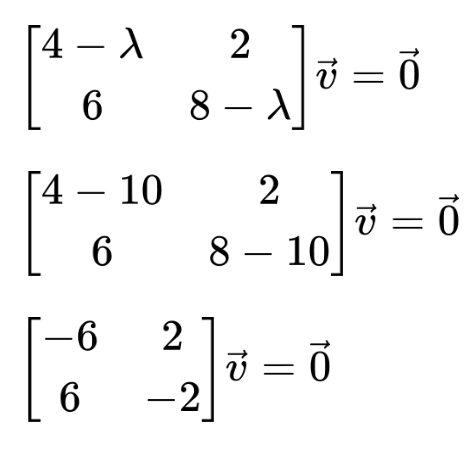
Step 2: Perform row echelon reduction.

1. Divide R₁ by -6.

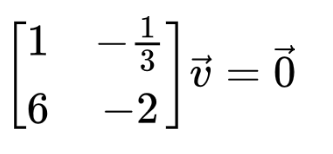
2. Subtract R₁ multiplied by 6 from R₂.

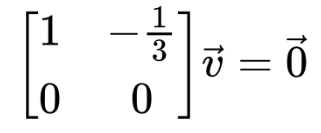
Step 3: Replace v and 0.

  
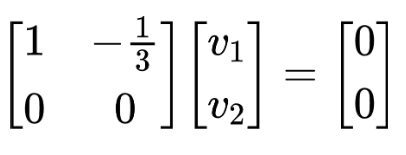
It becomes:

v₁ - v₂/ 3 = 0
v₁ = v₂ /3

According to the above equation: 

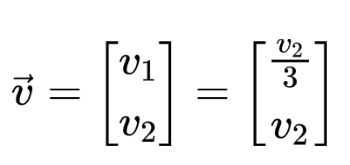
Letting v₂ = 1, the first eigenvector we get is:

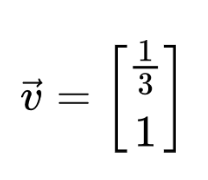
Step 4: Similarly, find the second eigenvector.

Swap R₁ with R₂

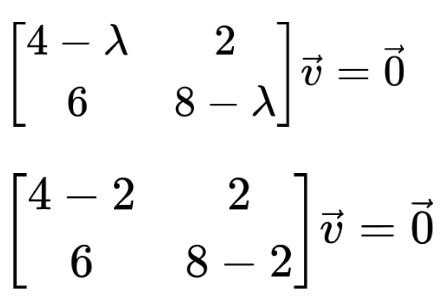
Multiply ⅓ with R₁ and subtract from R₂.

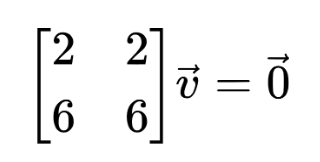
Divide R₁ by 6.

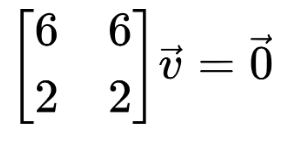
It becomes:
v₁ + v₂ = 0
v₁ = -v₂

According to the above equation:

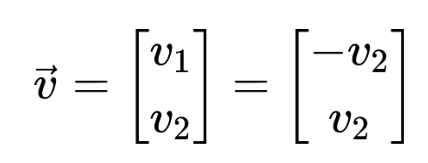
Letting v₂ = 1, the second eigenvector we get is:

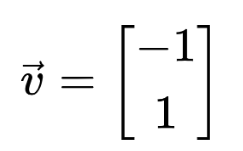
The eigenvector calculator will give an answer with all these steps.