To calculate result you have to disable your ad blocker first.
Exponent Calculator
To calculate n raise to the power of x (xn), enter the value of base and exponent in the given input boxes and hit the "calculate" button of this exponent calculator
Table of Contents:
Exponent Calculator
Exponents Calculator or e calculator is used in solving exponential forms of expressions. It is also known as raised to the power calculator.
Properties of exponents calculator:
This calculator solves bases with both negative exponents and positive exponents. It also provides a step by step method with an accurate answer.
What is an exponent?
An exponent is a small number located in the upper, right-hand position of an exponential expression (base exponent), which indicates the power to which the base of the expression is raised.
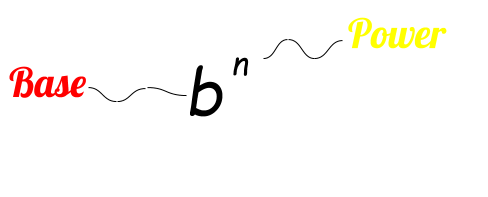
The exponent of a number shows you how many times the number is to be used in multiplication. Exponents do not have to be numbers or constants; they can be variables.
They are often positive whole numbers, but they can be negative numbers, fractional numbers, irrational numbers, or complex numbers. It is written as a small number to the right and above the base number.
Types:
There are basically two types of exponents.
Positive exponent
A positive exponent tells how many times a number is needed to be multiplied by itself. Use our exponent calculator to solve your questions.
Negative exponent
A negative exponent represents which fraction of the base, the solution is. To simplify exponents with power in the form of fractions, use our exponent calculator.
Example:
Calculate the exponent for the 3 raised to the power of 4 (3 to the power of 4).
It means = 34
Solution:
3*3*3*3 = 81
4 to the 3rd power = 81
Therefore the exponent is 81
2 raised to the power calculator.
Example:
What is the value of exponent for 2 raise to power 9 (2 to the 9th power)
It means = 29
Solution:
2*2*2*2*2*2*2*2*2 = 512
2 to the 9th power = 512
Therefore the exponent is 512.
Example:
How do you calculate the exponents of 5,6,7 to the power of 4?
It means = 54, 64, 74
Solution:
5*5*5*5 = 625
6*6*6*6 = 1296
7*7*7*7 = 2401
Therefore the exponents are 625, 1296, 2401.
How to calculate the nth power of a number?
The nth power of a base, let’s say “y”, means y multiplied to itself nth time. If we are to find the fifth power of y, it is y*y*y*y*y.
Some other solutions for the nth power calculator are in the following table.
| 0.1 to the power of 3 | 0.00100 |
| 0.5 to the power of 3 | 0.12500 |
| 0.5 to the power of 4 | 0.06250 |
| 1.2 to the power of 4 | 2.07360 |
| 1.02 to the 10th power | 1.21899 |
| 1.03 to the 10th power | 1.34392 |
| 1.2 to the power of 5 | 2.48832 |
| 1.4 to the 10th power | 28.92547 |
| 1.05 to the power of 5 | 1.27628 |
| 1.05 to the 10th power | 1.62889 |
| 1.06 to the 10th power | 1.79085 |
| 2 to the 3rd power | 8 |
| 2 to the power of 3 | 8 |
| 2 raised to the power of 4 | 16 |
| 2 to the power of 6 | 64 |
| 2 to the power of 7 | 128 |
| 2 to the 9th power | 512 |
| 2 to the tenth power | 1024 |
| 2 to the 15th power | 32768 |
| 2 to the 10th power | 1024 |
| 2 to the power of 28 | 268435456 |
| 3 to the power of 2 | 9 |
| 3 to the 3 power | 27 |
| 3 to the 4 power | 81 |
| 3 to the 8th power | 6561 |
| 3 to the 9th power | 19683 |
| 3 to the 12th power | 531441 |
| 3 to what power equals 81 | 34 |
| 4 to the power of 3 | 64 |
| 4 to the power of 4 | 256 |
| 4 to the power of 7 | 16384 |
| 7 to the power of 3 | 343 |
| 12 to the 2nd power | 144 |
| 2.5 to the power of 3 | 15.625 |
| 12 to the power of 3 | 1728 |
| 10 exponent 3 | 1000 |
| 24 to the second power (242) | 576 |
| 10 to the power of 3 | 1000 |
| 3 to the power of 5 | 243 |
| 6 to the power of 3 | 216 |
| 9 to the power of 3 | 729 |
| 9 to the power of 2 | 81 |
| 10 to the power of 5 | 100000 |
Exponent Rules:
Learning the exponent rules along with log rules can make maths really easy for understanding. There are 7 exponent rules.
Zero Property of exponent:
It means if the power of a base is zero then the value of the solution will be 1.
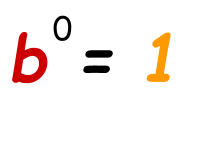
Example: Simplify 50.
In this question, the power of base is zero, then according to the zero property of exponents, the answer of this non zero base is 1. Hence,
50= 1
Negative Property of exponent:
It means when the power of base is a negative number, then after multiplying we will have to find the reciprocal of the answer.
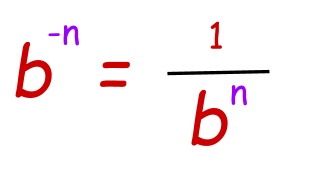
Example: Simplify 1/3-2.
We will first make the power positive by taking reciprocal.
1/3-2=32
32 = 9
Product Property of exponent:
When two exponential expressions having the same non zero base and different powers are multiplied, then their powers are added over the same base.
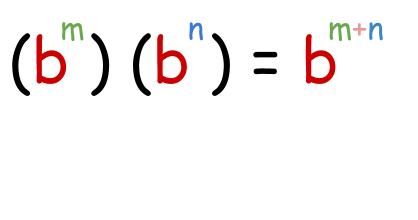
Example: Solve (26)(22).
As it is obvious, bases are the same so powers are to be added. Now
(26)(22) = 26+2
28 =2*2*2*2*2*2*2*2
=256
Quotient Property of exponent:
It is the opposite of the product property of exponent. When two same bases having different exponents are required to be divided, then their powers are subtracted.
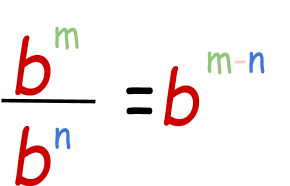
Example: Simplify 37 /32
37 / 32=37-2
35=3*3*3*3*3
= 243
Power of a Power Property:
When an exponent expression further has power, then firstly you need to multiply the powers and then solve the expression.
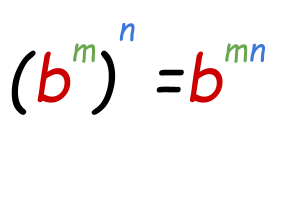
Example: Solve: ( x2)3.
Keeping in view the power of power property of exponents, we will multiply powers.
(x2)3=x2*3
= x6
Power of a product property:
When a product of bases is raised to some power, the bases will possess the power separately.
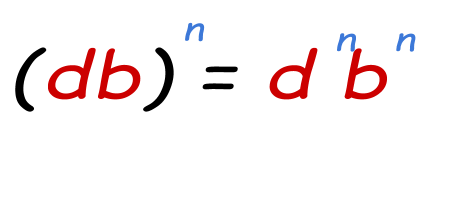
Example: Simplify (4*5)2
42 * 52=16*25
= 400
Power of a Quotient Property:
It is the same as the power of a product property. Power belongs separately to both the numerator and denominator.
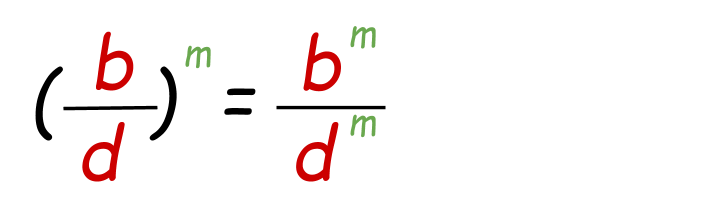
Example: Solve (2/3)2
(2/3)2=22 / 32
22 / 32=4/9
References:
- Mclph.umn.edu. 2020. What Is An Exponent?.
- Stapel, E., 2020. Exponents: Basic Rules | Purplemath.
- Math.com. 2020. Algebra Basics - Exponents - In Depth.
- Mathinsight.org. 2020. Basic Rules For Exponentiation - Math Insight.
- Analyzemath.com. 2020. What Are Exponents In Maths - Grade 7 Maths Questions With Detailed Solutions.