Hexadecimal Calculator

The hexadecimal calculator performs algebraic operations on the hex numbers. It can perform the basic 4 operations including addition, subtraction, multiplication, and division. 

It will give the answer in the hexadecimal number system. You will find all of the mathematical operations performed on the decimal form of the entered hex numbers. 

What are hexadecimal numbers?

Hexadecimal is a number system similar to decimal, binary, and octal number systems. It uses base sixteen (16). The sixteen hex digits include numerals from 0 to 9 and alphabets from A to F. 

The letter A stands for 10, B for 11, C for 12 so on. This number system is used in the different fields of computer. The main purpose of this system is that it compresses binary numbers to save space for better working. 

Algebraic operations on the hex numbers

The operations are performed as in the decimal number system. The difference comes where the conversions are involved. 

In the article below, we will go through each operation one by one. But before jumping on to the operations, let’s give a brief glance at the conversion of decimal to hex and hex to decimal. 

Converting decimals to hex:

Divide the number by 16 and note the quotient and remainder. Mark this remainder as one and find its hex equivalent. Now, take the previous quotient and repeat. Mark this remainder as two.

Keep doing this process until the quotient itself becomes smaller than 16. Let’s see an example.

Example:

Convert 1256₁₀ into hex system.

Solution:

Division	Quotient	Remainder in base ten	Remainder in base sixteen	Digit number
1256/16	78	8	8	0
78/16	4	14	E	1
4/16	none	4	4	2

Write the digits from bottom to top as 4E8₁₆. Use the decimal to hex converter instead.

Note: The digit numbers started from 0 because for the backward conversion, you have to raise these numbers as powers. Powers in such conversions start from 0. See the next heading.

Converting from hex to decimal

The hex numbers are converted into decimal numbers in the same way binary is converted into decimals. Find the place value of each hex number. Raise 16 to this power (place value) and multiply with the digit. Add all numbers.

Example:

Find the decimal value of DEF.

Solution:

Step 1: Find the place values.

• F is at 0’s place
• E is at 1’s place
• D is at 2’s place 

Step 2: Raise these values as powers and multiply with the digits.

• As F = 15₁₀, 15₁₀ x 16⁰ = 15₁₀
• E = 14₁₀, 14₁₀ x 16¹ = 224₁₀
• D = 13₁₀, 13₁₀ x 16² = 3328₁₀

Step 3: Add these numbers.

= 3328₁₀ + 224₁₀ + 15₁₀

= 3567₁₀

Now, it is time to dive into the arithmetic operations. Try hex to decimal converter.

How to add hex numbers?

Change the alphabets to their decimal equivalents and add the hex numbers. But before writing them, you have to change them into hex as the addition was in decimal numbers. 

Example of hex addition:

Add 1E4 and 33D.

Solution:

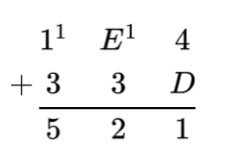
In this calculation, we first added 4 and D. As D = 13, then 4+13 = 17₁₀ which is 11₁₆. Taking 1 as carry to E. Then E = 14, so 14+1+3 =18₁₀ = 12₁₆. Lastly, 1+1+3 = 5₁₀ which is same in the hex system.

How to subtract hex numbers?

It is also similar to the hex addition. But you have to be careful in borrowing numbers. In hex subtraction, when you borrow 1 from the preceding number, you add 16 into the current number. Because 16 hex is equal to 10 decimal.

Example of hex subtraction:

Subtract 5AF from the F89.

Solution:

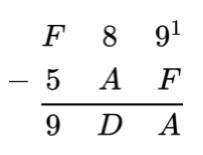
In the first column, 9 is smaller than F that is actually 15. On borrowing 1 from previous digit 8, the calculations you get are 9 + 16 - 15 = 10₁₀ = A₁₆. In the second row, borrowing is again required. 8 had become 7. So on borrowing, 16 + 7 - A = 16 + 7 - 10 = 14₁₀ = D₁₆. The last row has E in the first row because it was reduced during the previous borrowing. So, E - 5 = 14 - 5 = 9₁₀. It is the same in hex as well. 

How to multiply hex numbers?

It is quite difficult to perform multiplication on hexadecimal numbers. Every time a row is multiplied by a digit, conversions will be done as well as at the last during addition.

Example of hex multiplication:

Multiply 44A by FA.

Solution:

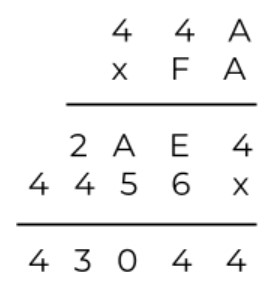
For the first row (44A x A):

A multiplied by A is actually 10 multiplied by 10. The answer 100₁₀ is converted into hex 64₁₆. The 4 remains at the bottom and 6 goes as a carry. Next A x 4 = 40₁₀. Now, add the 6 of carry in this 40₁₀, the answer is 46₁₀ = 2E₁₆. E is at the bottom and 2 again goes as carry. As A x 4 = 40₁₀ + 2₁₀ = 42₁₀ = 2A₁₆. The answer is 2AE4.

For the second row (44A x F):

A x F = 10₁₀ x 15₁₀ = 150₁₀ = 96₁₆. Keep 6 in the bottom and put 9 as the carry. F x 4 = 15₁₀ x 4₁₀ = 60₁₀. Add 9₁₀, it becomes 69₁₀ which is 45₁₆. Lastly, use the same knowledge to multiply 4 x F again and add carry. The final answer of this row is 4456. 

Add 2AD4 and 4456 using the addition method.

How to divide hex numbers?

The best way to do division on hex numbers is to convert hex numbers into decimal numbers, perform long division on it and then convert back. Or the other way is to divide using the hex number themselves. 

For hex numbers, it is better to make a multiplication table of divisors and then use those values to perform long division.

The example below is of hex numbers.

Example of hex division:

Divide DACE by E.

Solution:

Step 1: Make the multiplication table.

Multiple	Hex multiple	Decimal value
E x 1	E	14
E x 2	1C	28
E x 3	28	42
E x 4	38	56
E x 5	46	70
E x 6	54	84
E x 7	62	98
E x 8	70	112
E x 9	7E	126
E x 10 / E x A	8C	140

Step 2: Perform long division.

= DACE / E

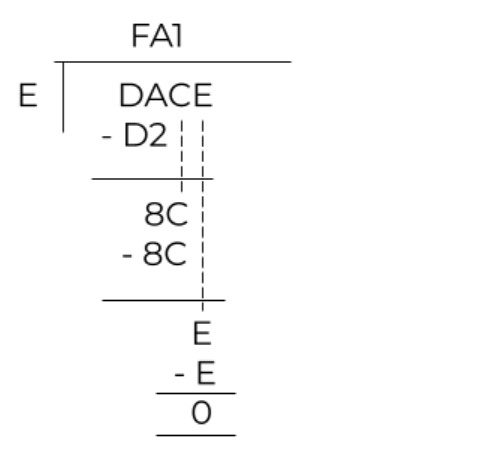
Since D < E then make a pair of DA. DA₁₆ = 218₁₀. We don’t have this big number. This means multiplying E with numbers greater than A.

If we multiply E with F, we get D2. In decimal language, it is 14 x 15 = 210.

So put this under DA. On subtracting D2 from DA, the answer is 8. Now bring C down. To divide 8C by E, we multiply E by A. (see the table).

In the end, only E is left. According to the multiplication table we made, use E.