Polynomial Long Division Calculator

Polynomial Long Division Calculator

Divide the polynomials using the polynomial long division calculator with steps to find the results with solution and remainder. This is an online tool to solve polynomials in the simplest form.

 To learn more about the polynomials and their division, continue reading.

What are polynomials?

Polynomials can be explained better by showing some examples. 

• X² - 2x + 3
• 10x
• X⁴ + 7
• xy - y² - 5

All of these are polynomials. Each contains at least one variable. It is an algebraic expression and usually contains many terms. There are three basic types.

Monomials:

It contains only one term. For example: x² , 3x , -2z³ 

Binomials:

Binomials contain two terms separated by a plus or minus sign. E.g 2x - 1, 4x + 2y

It can consist of two variables or one variable as well. The only condition is that it has to have 2 terms. 

Polynomials:   

Lastly, an algebraic expression with three or more terms is referred to as a polynomial because poly means several. Such as 8x² - 7y + 3x⁴ and z⁹ - 3z⁸ - 5z⁷ + 6. 

How to perform polynomial long division?

The method is very similar to the basic arithmetic long division. The following are the important steps:

1. Arrange the polynomials in standard polynomial form.
2. Write the numerator under the radical sign.
3. After that, write the denominator outside the symbol.
4. Find the suitable quotient to divide the first term of the numerator.
5. Keep dividing until completely solved or a remainder is obtained. 

Finding the suitable quotient in binomials and polynomials:

You can use a handy trick to find a suitable quotient in less time. The trick is

“Divide the first term of the numerator with the first term of the denominator. Multiply the quotient with the complete denominator and use it in the long division.”

For example, you want to divide 8x2 -6x + 7 by 4x - 1. First, write in the syntax.

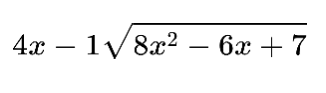
Now take the first terms of both polynomials and divide the higher value by the lower.

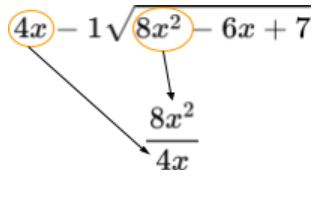
The answer is 2x. Now, multiply the denominator by 2x and place it under the numerator. 

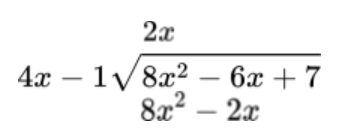
Let’s see a full solved example to see the manual method of performing polynomial long division besides using the calculator. 

Example:

Solution:

Step 1: Write the values in the designated place. 

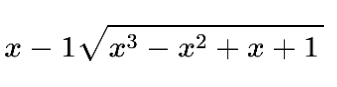
Step 2: Find the suitable quotient using the above-mentioned method.

The quotient is x2. 

Step 3: Multiply it to the “x - 1” and continue division.

The denominator becomes x3 - x2.

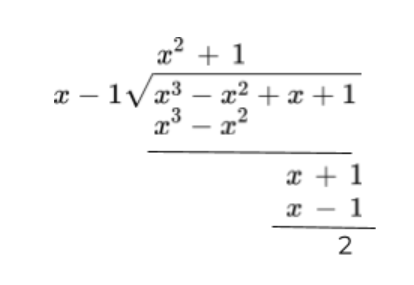
The remainder is 2.