Continued Fraction Calculator

Continued Fraction Calculator

Continued fraction calculator is a mathematical tool that helps to find a series of numbers by using fraction numbers. It gives the continued fraction of any fraction by hitting the calculate button.

What is a Continued Fraction?

A Continued fraction is a unique way to represent the fractional number in a finite series of numbers. More simply, it writes every fraction number using the remainder theorem to write the series in the addition of quotient and fraction of remainder over divisor.

Then take the reciprocal of the remainder and the divisor. Again, make the series of numbers by using the remainder theorem while continuing the process at that time if the remainder is equal to 1.

Formula of Continued Fraction:

The continued fraction can be determined by using the below formula.

r = a0 + 1/(a1+1)

Where

• a0 = shows the first term.
• a1 = represent the next term.

The general formula of the continued fraction can be stated as,

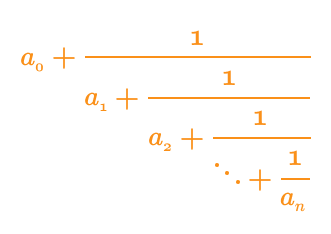
How to evaluate the continued fraction?

The above continued fraction calculator will help you to determine a series of generalized continued fractions. Here, we solve some examples to learn how to perform calculations manually.

Example 1:

Find the Continued fraction of the given fraction that is “75/7”.

Solution:

Step 1: Write the given fraction.

Simple fraction = 75/7,                            Continued fraction =?

Step 2: Put the values in the continued fraction formula and simplify the terms.

Simple fraction = 75/7

Divide the terms and set them by using the remainder theorem.

75/7 = 10 + (5/7) ---------> (i)

Now take the reciprocal of the “5/7” and again divide the number.

Reciprocal of 5/7 = 7/5

Now, the solution of the above.

7/5 = 1+ (2/5) ---------> (ii)

Again, take the reciprocal of “2/5” and repeat the above process.

Reciprocal of 2/5 = 5/2

Now, divide the above term again and we get.

5/2 = 2 + (1/2) ---------> (iii)

Step 3: We get the Continued fraction of the given fraction by using the eq (i, ii, iii).

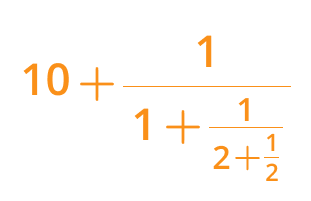
Continued fraction = [10; 1, 2, 2]