Cramer's rule calculator

D is the determinant of main matrix.

Cramer's rule calculator efficiently solves the simultaneous linear equations and instantly finds the value for the variables in the equation. It applies the Cramer’s rule for 2x2, 3x3, and 4x4 matrices as well.

If you know how to use Cramer’s rule on 2x2 system, and looking for the implementation of Cramer’s rule on 3x3 or 4x4 systems, then continue reading the next sections.

What is Cramer’s rule?

Cramer’s rule is a method to evaluate the value of given unknown variables in linear equations. It is proposed by Gabriel Cramer in 1750. By using this rule, one can solve simultaneous linear equations with much ease.

How to solve linear equations with Cramer’s rule?

To solve simultaneous linear equations using Cramer’s rule, follow the below steps.

Example:

Solve the equations given below for x, y, and z.

2x+3y+5z=10

5x+3y+2z=12

x+5y+0z=8

Solution:

Step 1: By using the coefficients, variables, and constants, develop a matrix as shown below.

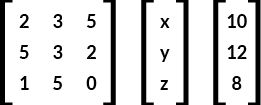
Step 2: Find the determinant of the main matrix. Suppose main matrix is equal to D.

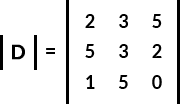
= 2[(3×0)-(2×5)] - 3[(5×0)-(2×1)] + 5[(5×5)-(3×1)]

= 2(0-10) - 3(0-2) + 5(25-3)

= -20 + 6 + 110

|D| = 96

Step 3: Construct x, y, and z matrices by replacing the x, y, and z columns of the main matrix D by the constant matrix respectively.

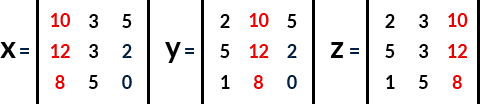
Step 4: Take the determinant of all of the three new matrices x, y, and z.

D_x = 10[(3×0)-(2×5)] - 3[(12×0)-(2×8)] + 5[(12×5)-(3×8)]

D_x = -100 + 48 + 180

D_x = 128

D_y = 2[(12×0)-(2×8)] - 10[(5×0)-(2×1)] + 5[(5×8)-(12×1)]

D_y = -32 + 20 + 140

D_y = 128

D_z = 2[(3×8)-(12×5)] - 3[(5×8)-(12×1)] + 10[(5×5)-(3×1)]

D_z = -72 - 84 + 220

D_z = 64

Step 4: Apply the Cramer’s rules and place the values.

x = D_x/D = 128/96

x = 1.33

y = D_y/D = 128/96

y = 1.33

z = D_z/D = 64/96

z = 0.67

So, we got x = 1.33, y = 1.33, and z = 0.67 after applying Cramer’s rule on the given 3x3 equation.