Five (5) Number Summary Calculator

Five number summary calculator is an online tool that calculates a statistical summary of given numbers. The summary includes:

1. Minimum number
2. Maximum number
3. First quartile
4. Median
5. Third quartile

Moreover, the 5 number summary calculator also calculates the inter quartile, ascending order, and descending order for the given input.In this post, we will explain how to calculate 5 number summary with an example.

How to calculate five number summary?

Here are the steps to compute five number summary:

• Write down the list of numbers.
• Arrange the numbers in ascending order.
• Write down the maximum and minimum values from this list of numbers.
• Find out the median from this list. If the group of data is odd, median will be the middle number. If the data consists of even set of numbers, then take the two middle values and divide them by two to get the median.

• Place the values in the parenthesis except median.

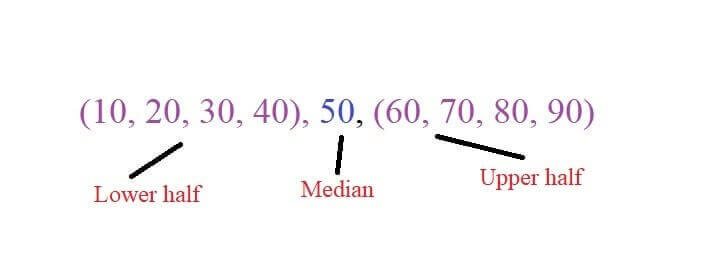
• Find the median in the lower half to get the 1^st quartile. Similarly, find the median in the upper half to get the 3^rd quartile.
• Write down all the terms you calculated to make a five (5) number summary.

Example:

Calculate the 5 number summary in an un-arranged data set given below. (more examples at allmath)

4, 1, 9, 2, 6, 3, 7, 11, 5

Solution:

Step 1: Write down the list of numbers.

4, 1, 9, 2, 6, 3, 7, 11, 5

Step 2: Arrange the numbers in ascending order.

1, 2, 3, 4, 5, 6, 7, 9, 11

Step 3: Write down the maximum and minimum values from this list of numbers.

Maximum number = 11

Minimum number = 1

Step 4: Find out the median from this list. The set of data we are working on, consists of odd set of numbers. So, we will only pick the middle value from the data set.

Median = 5

Step 5: Place the values in the parenthesis except median.

(1, 2, 3, 4), 5, (6, 7, 9, 11)

Step 6: Now it’s time to find the quartiles. Find the median in the lower half to get the 1^st quartile. Similarly, find the median in the upper half to get the 3^rd quartile.

Q1 = (2 + 3)/2 = 2.5

Q3 = (7 + 9)/2 = 8

Step 7: Write down all the terms you calculated to make a 5 number summary.

Minimum = 1

Maximum = 11

Median = 5

Q1 = 2.5

Q3 = 8