To calculate result you have to disable your ad blocker first.
Quartile Calculator
Input all the values of the group, separated by commas. Then click calculate to find information related to Quartiles.
Table of Contents:
Quartile Calculator
Quartile calculator is an online statistical calculator that finds the value of a quartile in a given range. It is a very easy-to-use tool to quickly get the quartile range sorted out for your statistics problems.
This IQR calculator finds the:
- Interquartile Range (IQR)
- 1st Quartile (Q1)
- 2nd Quartile (Q2)
- 3rd Quartile (Q3)
This tool is also referred to as the mean median and mode calculator because it calculates the quartile values by calculating the median of the lower range and upper range of the values.
Definitions
Here we will learn definitions for the terms you read above.
What is a quartile?
“A quartile is a type of quantile which divides the number of data points into four more or less equal parts, or quarters.”
A quartile represents the specific part of a data set. A set of data contains:
1st quartile
The first quartile represents the 25th percentile of the data set. It divides the data into a lower 25 percent and also known as the lower quartile. It is denoted by Q1.
2nd quartile
The second quartile represents the 50th percentile of the data set. It divides the data into half or 50 percent and is also known as the median. It is denoted by Q2.
3rd quartile
The third quartile represents the 75th percentile of the data set. It divides the data into 75 percent from the remaining data set and is also known as the upper quartile. It is denoted by Q3.
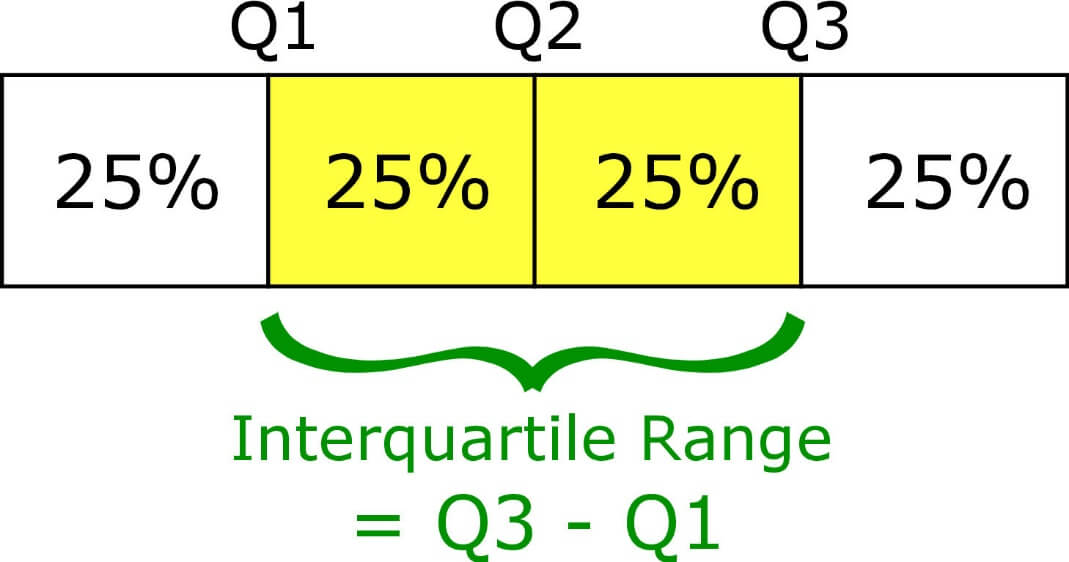
Interquartile range
It is the difference between the upper quartile Q3 and the lower quartile Q1. The interquartile range is denoted by IQR. It is also known as H-spread in statistics.
Formula to calculate Quartiles
The general formula to calculate quartile is:
Qj=j/4 (n + 1)th term
Where “j” is the quartile number i.e 1, 2, and 3. Note that this formula tells the position of the quartile value and not the value itself.
For interquartile range
The interquartile range formula can be stated as:
IQR = Q3 – Q1
How to calculate quartiles?
Example:
For the following set of data, calculate all quartiles and interquartile range.
13, 5, 3, 7, 9, 15, 17, 11
Solution:
Step 1: Arrange the data into ascending order.
= 3, 5, 7, 9, 11, 13, 15, 17
Step 2: Count the values
There are 8 values
Step 3: We will calculate quartiles one by one
- The first quartile (Q1)
Qj=j/4 (n + 1)th term
Q1 = ¼ (8 + 1)th term
Q1 = ¼ (9)th term
Q1 = 2.25 th term
Solving to find the value
= 2th term + 0.25 ( 3rd - 2nd)
= 5 + 0.25 (7-5)
= 5 + 0.25 (2)
= 5 + 0.5
= 5.5
- The second Quartile (Q2)
Qj=j4 (n + 1)th term
Q2 = 2/4 (8 + 1)th term
Q2 = 2/4 (9)th term
Q2 =4.5th term
Solving to find the value
= 4th term + 0.5 ( 5th - 4th)
= 9 + 0.5 (11 - 9)
= 9 + 0.5 (2)
= 9 + 1
= 10 (this is also median)
- Third quartile (Q3)
Qj=j/4 (n + 1)th term
Q3 = 3/4 (8 + 1)th term
Q3 = 3/4 (9)th term
Q3 = 6.75th term
Solving to find the value
= 6th term + 0.75 ( 7th - 6th)
= 13 + 0.75 (15 - 13)
= 13 + 0.75 (2)
= 13 + 1.5
= 14.5
Step 4: Now calculate interquartile range.
IQR = Q3 – Q1
= 14.5 - 5.5
= 9