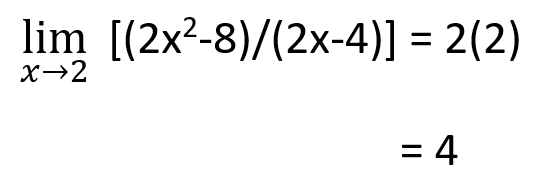L'hopital's Rule Calculator

L’hopital’s rule calculator is used to calculate the limit value of the indeterminate function. This l’hopital calculator finds the result with steps in a fraction of seconds.

What is L'hopital's Rule?

In calculus, L’hopital’s rule is a fundamental theorem of limits that is used to evaluate indeterminate forms i.e., 0/0 or ∞/∞ during the calculation of limits.

When a function form 0/0 or ∞/∞ after putting the limit value then the l’hopital’s rule of limit is applied. According to this rule, find the derivative of the numerator and denominator of the function and apply the limit value again.

If the function again forms 0/0 or ∞/∞, then repeat the process again and again until you got the result.

L'hopital's Rule Formula

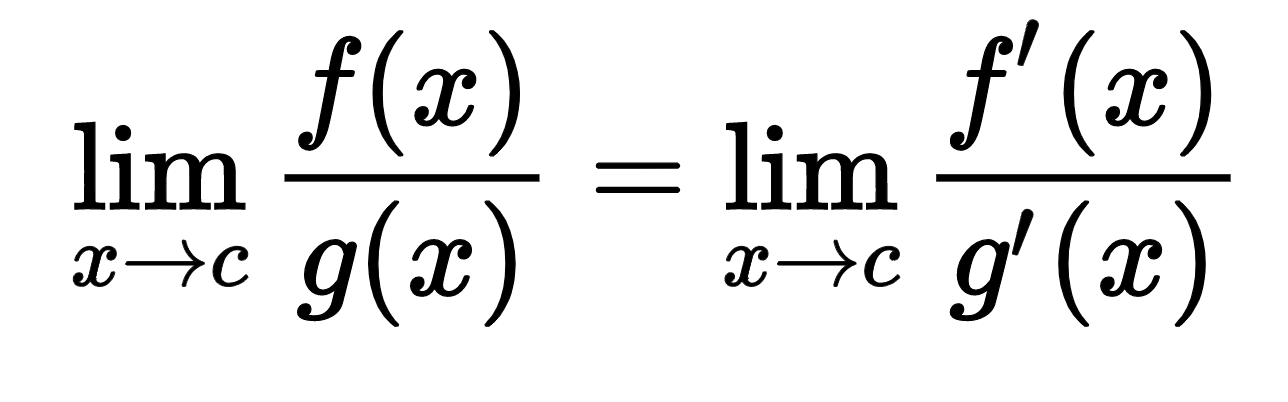
How to find the limits by using L'hopital's rule?

Below is an example of L'hopital's rule solved by the manual method.

Example

Find the limit of (2x²-8)/(2x-4) when “x” approaches 2.

Solution

Step 1: Apply the notation of limits on the given function.

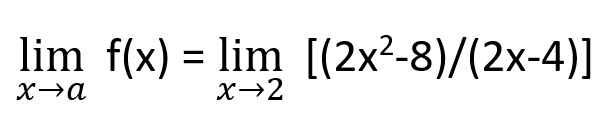
Step 2: Apply the value of the limit.

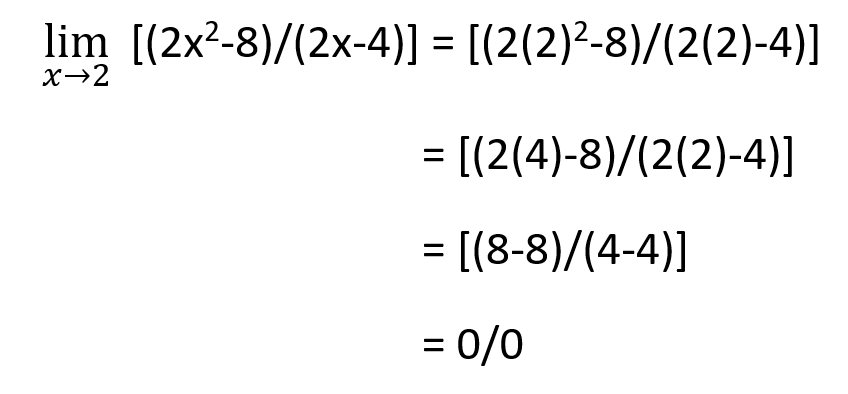
Step 3: Use L’hopital’s rule of limits as the given function form 0/0 after applying the limit.

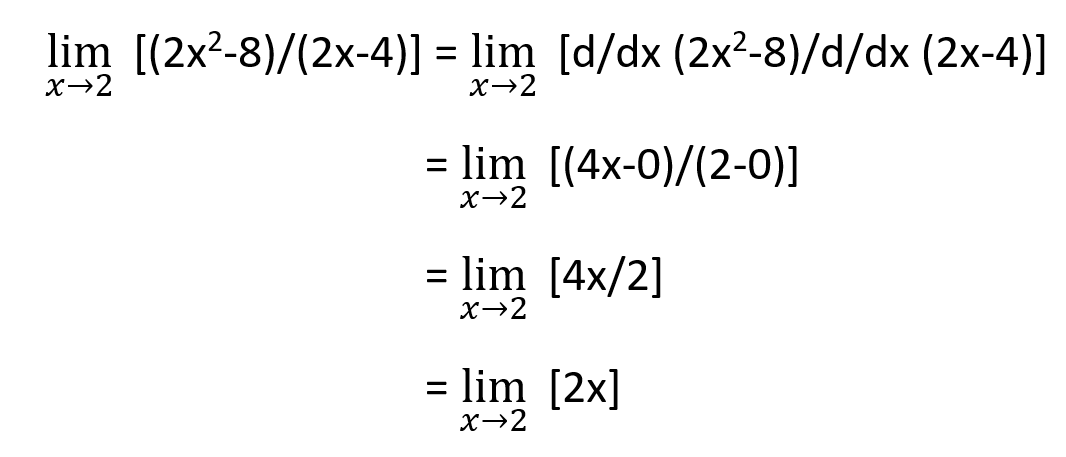
Step 4: Apply the limit value again.