To calculate result you have to disable your ad blocker first.
Limit Calculator With Steps
Enter the function and other values in the given input boxes. Hit the Calculate button to evaluate the limit with steps using limits calculator.
Table of Contents:
Limit Calculator
Limit calculator is used to evaluate the limit functions with respect to a specified variable. The variable could be x, y, z, etc. The limits calculator solves the limits with steps and shows you each phase of the calculation.
What are limits?
The idea of a limit of a function is vital to the study of calculus. It is used in describing some of the significant theories in calculus such as the definite integral of a function, a derivative of a function, and continuity.
The limit of a function f(x) defines the behavior of the function near to a specific x value. It does not essentially provide the value of the function at x.
\( \lim_{x \to c} f(x) = L \)
It can be read as the limit of f of x as x approaches c equals L.
The limit solver above can evaluate both right-hand and left-hand limits.
Limits formulas – Limits rules
Below, we have provided laws of limits.
Notation of limit
\( \lim_{x \to c} f(x) = L \)
Left-Hand limit
![]()
Right-Hand limit
![]()
Limits of trigonometric functions
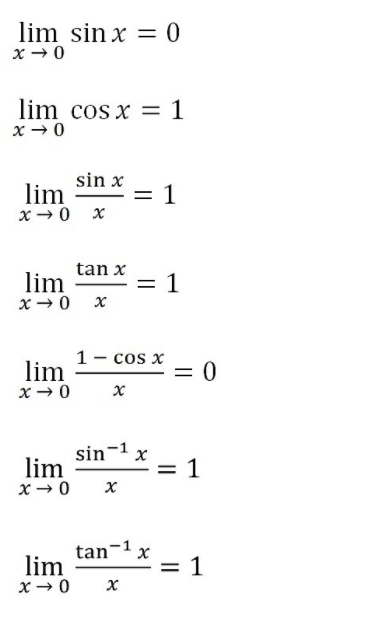
Limits of logs and exponential functions
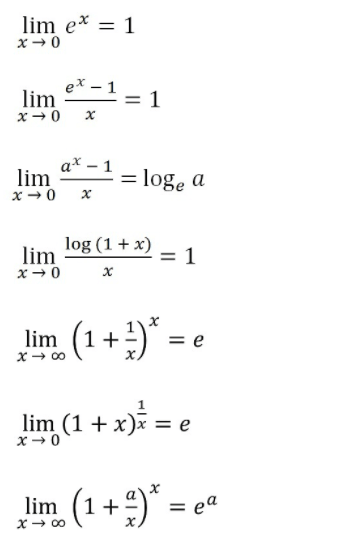
Limits of form ∞
![]()
Limits of xn
Checking if the limit exists
To check if the limit exists for f(x) at x = a, we check if,
Left hand limit = Right hand limit = f(a)
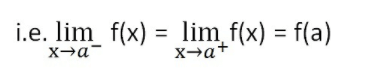
L'hospital's rule
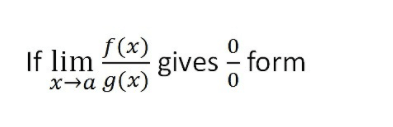
Where,
f(a) = 0
g(a) = 0
Then,
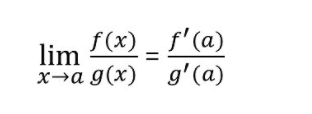
You can use our l'hopital's rule calculator to verify the answer of any limit function.
Limits sum rule
![]()
Limits product rule
![]()
Limits quotient rule
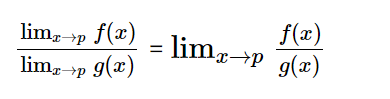
Limits power rule
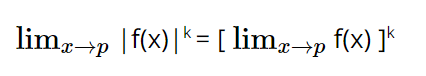
Constant rule of limits
The limit of a constant function is equal to a constant.
How to evaluate limits?
The limit calculator is designed specifically for the purpose of limit evaluation. But, we will explain the manual method to evaluate limits. The below example illustrates the handbook method with steps.
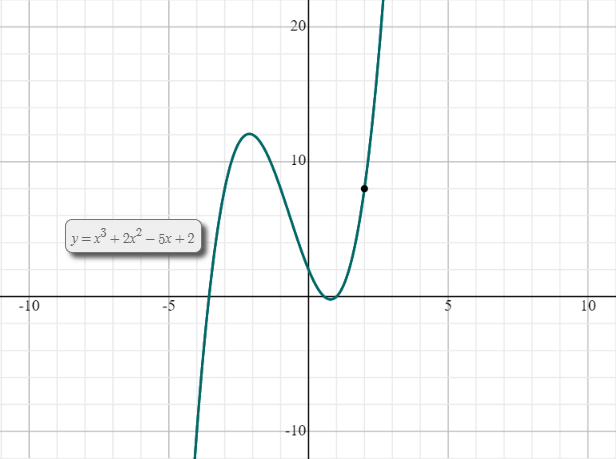
Example:
Evaluate:
\( \lim_{x \to 2} (x^3+2x^2-5x+2) \)
Solution:
Step 1: Write down the value.
\( \lim_{x \to 2} (x^3+2x^2-5x+2) \)
Step 2: Apply the limit function to each element.
\( \lim_{x \to 2} (x^3) + \lim_{x \to 2} (2x^2) - \lim_{x \to 2}(5x) + \lim_{x \to 2}(2) \)
Step 3: Take the coefficients out of the limit function.
\( \lim_{x \to 2} (x^3) + 2 \lim_{x \to 2} (x^2) - 5 \lim_{x \to 2}(x) + \lim_{x \to 2}(x) + 2 \)
Step 4: Apply the limit by placing \( x -> 2 \) in the equation.
\( = 1(2^3)+2(2^2)-5(2)+2 \)
\( = 8+8-10+2 \)
\( = 8 \)
so, \( \lim_{x \to 2} (x^3+2x^2-5x+2) = 8 \)
Here is the graph plotted for the above function.