Permutation Calculator

Permutation Calculator 

The mera’s permutation calculator gives the unrepeated permutation sets for the given n and r. It uses the accurate formula and method which you can find below the result by clicking on the “show steps”.

What is permutation?

Permutation and combination are two methods to make groups out of a set. Both are somewhat similar to each other. In Permutation, you basically arrange elements in every possible way keeping the order of elements important.  

There are two types of permutations: repeated and without repetition. The permutation calculator finds the arrangements of elements without repetition. 

Permutation formula:

Both types of permutation arrangements are found using separate formulas. For non-repeated permutation formula is:

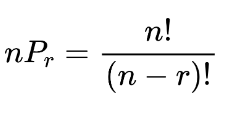
Where n is the total number of elements and r is the number of elements you want in each subset. 

This formula can be understood with the help of an example. Consider you have 6 different numbers in a set and you are allowed to pick 2 out of the 6 to solve a riddle.  You use the permutation formula to know how many possible pairs you can choose from. 

Remember that order or sequence is important in permutation not in combination. In your case, only 2 elements were to be taken. But if you consider taking all 6 elements in an order then the number of sequences or subsets will grow large because now you have more numbers to adjust.

For instant:

• (1) has only one possibility. 
• (1,2) has two possibilities i.e (1,2)(2,1)
• (1,2,3) has six possibilities i.e (1,2,3)(3,2,1),(2,1,3)(1,3,2)(3,1,2)(2,3,1)

Note: It is simply factorial of n.

So when the r increases so do the permutation subsets. 

The formula for repeated permutation is 

_np_r = p^r

How to find permutation?

Calculate the number of things or elements you have to choose from. Take its factorial. After this, subtract the r from n and find its factorial as well. At the last, divide the n! value with this value. 

Example: 

If there are 8 elements in a set then find the permutation for r=4.  

Solution:

Use the formula:

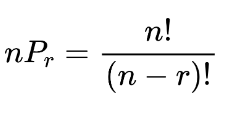
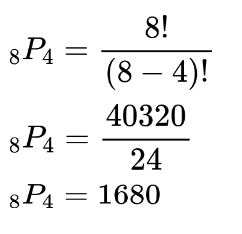
There are 1680 subsets of 4 elements for this particular set.