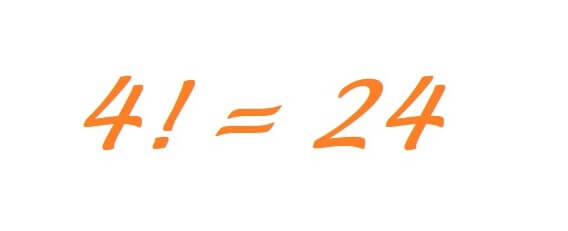To calculate result you have to disable your ad blocker first.
Factorial Calculator
Enter the number and click the calculate button to find the factorial
Table of Contents:
Factorial formula
The formula for factorial can be stated as:
n!=∏k=1nk
Where:
n represents the number of objects.
Factorial calculator is an online calculator that calculates the factorial of a given integer. It can be used to determine the number of ways in which a certain number of items can be arranged. For example:
If you have 4 dresses in your closet, and want to know the number of ways these dresses can be arranged. Simply calculate the factorial of 4.
It means, 4 dresses can be arranged in 24 ways in the closet.
Here, we will dive into factorial definition and factorial formula. Moreover, we will explain how to find factorial, and how you can use factorial calculator to calculate factorial for various integers.
How to use our factorial calculator?
Using above calculator to find factorial is much easier than to calculate it manually. It really saves the time and lets you calculate the n-factorial in no time. To use this calculator, follow the steps below:
- Enter the number in the given input box.
- Hit the Calculate button to get the factorial of given number.
- Use the Reset button to enter new value for the next calculation.
By following above steps, you can calculate the zero factorial, 6/4/8/7 factorial, negative factorial or factorial for any given integer.
What is a factorial?
Factorial definition according to Wikipedia is,
“In mathematics, the factorial of a positive integer n, denoted by n!, is the product of all positive integers less than or equal to n.”
n! = n × (n - 1) × (n - 2) × (n - 3) × (n - 4) × . . . × 3 × 2 × 1
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720
The exclamation sign (!) is used to denote the factorial.
In other words, factorial is the number of ways in which n objects can be arranged.
Some people mistakenly regard the factorial as highest common factor, but HCF is totally another concept. HCF is calculated by getting the highest common factors while factorial is calculated by multiplying the integer by the numbers that are less than original number.
How to calculate factorial?
Factorial calculation is very simple. In most cases, it doesn’t require the above formula. Whatever the number you have, simply multiply it with the numbers that are less than the original number.
Follow these steps to calculate factorial of an integer:
- Write down and identify the number n.
- Multiply n with the number that is less than i.e., if n is 4, multiply it with 3.
- Now multiply the result with the next lower number. i.e.,
- Continue multiplying factorials with the next lower number till
A real world example can help to understand how to calculate the factorial of an integer. Let’s solve some real world problems to grasp the concept.
Example 1:
In how many different ways the word MeraCalculator can be arranged using its letters?
Solution:
Step 1: Write down and identify the number n.
There are total 14 letters in the word MeraCalculator.
So, n = 14.
Step 2: Multiply n with the numbers that are less than n.
n! = 14 × 13 × 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
Step 3: Multiply all integers in the equation and get the result.
n! = 87178291200
So, there are total of 87178291200 ways in which the word MeraCalculator can be arranged using its letters.
Example 2:
Find the number of ways in which diamonds can be arranged in a standard deck of playing cards?

Solution:
Step 1: Write down and identify the number n.
There are total 13 diamond cards in a standard playing deck of cards.
So, n = 13.
Step 2: Multiply n with the numbers that are less than n.
n! = 113 × 12 × 11 × 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
Step 3: Multiply all integers in the equation and get the result.
n! = 6227020800
So, there are total of 6227020800 ways in which the diamond cards of a standard playing deck can be arranged.
What is a factorial of 10?
Factorial of 10 can be calculated as:
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
10! = 3628800
How do you calculate 5 factorial?
To calculate the factorial of 5, multiply it with all the numbers that are less than 5.
5! = 5 × 4 × 3 × 2 × 1
5! = 120
How do you calculate 7 factorial?
To calculate the factorial of 5, multiply it with all the numbers that are less than 5.
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1
7! = 5040
What is the factorial of zero?
According to the empty product rule,
Factorial of zero = 1
0! = 1
What are real life applications of factorial?
Some of the practical applications of factorial are:
- If you have to arrange some of your friends for sitting, then you can find out easily, in how many ways you can arrange it if you use the factorials.
- If you have to pack the shirts for your next trip, you can use factorials to find out how many shirts you can pack in a specific space.
- Using factorials, you can find the place of a word in a dictionary.
- One of the most significant and handy real-world application of factorial is to calculate the number of days in a year or number of minutes in a month, etc.
Factorial table
The below factorial table demonstrates the factorial values from 0 to 15.
| Number (n) | Factorial (n!) |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |