Scientific Notation Calculator

Also known as the exponential notation calculator, this tool is used to perform basic math operations on two numbers. These numbers should be in scientific notation.

You can enter the coefficients and exponents in this calculator separately and have a choice of 4 mathematical operations. 

Moreover, this tool also works as a scientific notation conversion calculator. It finds the engineering, E, and standard form of the calculated answer. 

What is scientific notation?

It is the scientific way of writing numbers. In this way of writing, most of the number is represented as a power of ten. Such as;

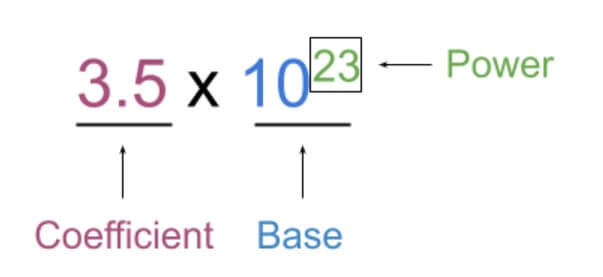
We deal with small amounts on a daily basis. However, scientists often have to deal with extremely small or extremely large numbers.

So for this purpose, it was necessary to devise a notation that could make such numbers easily usable in calculations.

To write the standard form in scientific notation, use the standard form calculator.

Mathematical Operations on Scientific notation

Under this heading you will learn about;

• Adding scientific notation
• Subtracting scientific notation
• Multiplying scientific notation
• Dividing scientific notation

All of the above topics will be explained with the help of examples.

How to add and subtract scientific notation?

When you add or minus two scientific notations, it is important to have the bases of the same power. If the exponents are not the same, they are modified in a way that they become equal. 

After that, the operation is performed on the coefficients. The common base is written in front of the calculated number.

Example 1:

Add the following numbers: 3.1 x 10² and 2 x 10².

Solution:

Since the exponents are the same, we will simply have to add the coefficients. 

= 3.1 + 2 = 5.1

Hence, the answer will be 5.1 x 10².

Example 2:

Subtract 5 x 10⁸ from 12 x 10⁸.

Solution:

Powers are same, so;

= 12 - 5 = 7

The answer is 7 x 10⁸.

Example 3:

Add the number 8.2 x 10³ and the number 12 x 10².

Solution:

In this example, the powers are different. One is 3 and the other is 2. You can select any of the two to make it equal to the other.

If we were to change the power of 8.2 x 10³, to 2, it would be like;

= 82 x 10²

On the other hand, if we modify the second number such that its power is 3, the new number will be;

= 1.2 x 10³.

You can use any one of the new numbers while the second number should be original. Find the sum of these numbers using the adding scientific notation calculator.

How to multiply and divide scientific notations?

While multiplying scientific notation numbers;

1. Coefficients are multiplied.
2. Powers are added

But when you are dividing;

1. Coefficients are divided.
2. Powers are subtracted. 

To clear any confusion, see the examples ahead;

Example 4:

What will be the answer if you multiply 1.9 x 10⁴ with 15 x 10⁷.

Solution:

Separate the coefficients and bases.

= (1.9 x 15) x (10⁴ x 10⁷)

= 28.5 x 104+7

= 28.9 x 10¹¹

To verify the answer or find its standard form, enter these numbers in a multiplying scientific notation calculator.

Example 3:

Divide 22 x 10⁴ by 2 x 10³.

Solution:

Do the same as the previous example.

= (22/2) x (10⁴/10³)

= 11 x 10^4-3

= 11 x 10¹

It can also be written as;

= 1.1 x 10²