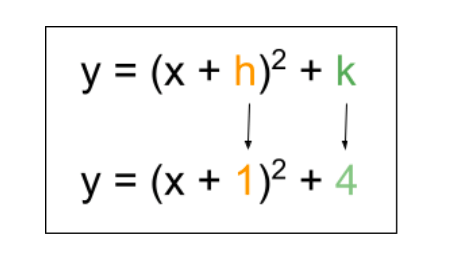Vertex Form Calculator

Vertex Form Calculator 

The vertex form calculator is used to find the vertex and y-intercept for a parabola. You can find the vertex for a standard quadratic form and vertex form of a parabola.

What is a vertex?

A vertex is the intersection point of the x and y coordinates of a parabola. It is the extremal point on its graph. It can be a minimum or maximum point.

The point is generally written as p(h,k). Here h is the x-coordinate and k is the y-coordinate.

Vertex formula:

Vertex is calculated from two types of equations: standard and vertex form. 

For standard form (y = ax² + bx + c):

h = -b/2a

k = c - b²/(4a)

(Alternatively, you can convert standard form into vertex form to identify the values.)

For vertex form (y = a*(x-h)² + k) :

Simply identify h and k. 

How to calculate the vertex of a parabola?

Example: 

Find the vertex for the equation:

y = 3x² + 2x + 5

Solution:

Step 1: Complete the square:

y = x² + 2x + 5

y - 5 + 1 = x² + 2x +1 (Adding 1 to the both sides)

y - 4 = (x + 1)²

y = (x + 1)² + 4

Now it is in vertex form.

Step 2: Identify h and k: