Resultant Force Calculator

Resultant force Calculator 

The resultant force calculator finds the magnitude and the direction of the resultant force. You can find the resultant for up to 2 force vectors.

If you have three vectors e.g a, b, and c, first enter the a and b vectors and then add the resultant vector of a and b and the c vector. 

What is the resultant force?

The resultant force is the net force acting on an object that is under multiple forces. Since force is a vector quantity, the resultant force has both magnitude and direction.

The resultant force can be displayed in the vector form as follows:

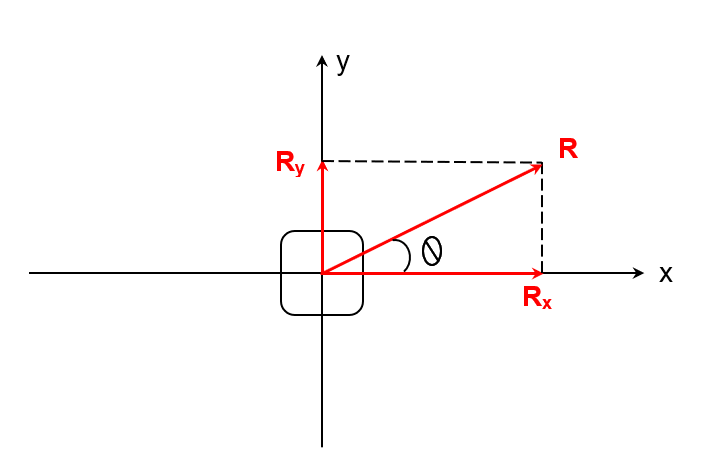
Resultant force formula:

There are different formulas for both magnitude and direction. 

For magnitude:

For magnitude, it is important to know the angle between the vectors.

And for direction/angle: 

Typically for finding the magnitude, the angle is calculated first. 

How to find the resultant force?

Example:

A car is being pushed by 10 newtons in the forward direction (0^o) and by 7 newtons from a 90 degrees angle.

Solution:

Step 1: Identify the values.

Magnitude of F₁ = 10N 

Magnitude of F₂ = 7N

Angle of F₁ = 0^o

Angle of F₂ = 90^o

Step 2: Find the x and y components of the resultant force.

X-component of F₁= 10cos(0) = 10

Y-component of F₁ = 10sin(0) = 0

X-component of F₂ = 7cos(90) = 0

Y-component of F₂ = 7sin(90) = 7

Step 3: Find summation fx and fy.

Σfx = 10 +0 = 10

Σfy = 0 + 7 = 7

Step 4: Find the angle.

θ = tan^-1 (7/10)

θ= tan^-1 (0.7)

θ_R = 34.99^o ≈ 35^o

Step 5: Put the values in the magnitude formula.

|R| = ½ [(10)² + (7)² - cos (35)]

|R| = ½ [100 + 49 - 0.819… ]

|R| = ½ [ 149 - 0.819… ]

|R| = ½ [ 148.093… ]

|R| = 12.2 N