How to calculate work done using its formula?
Publish Date:Before diving into this topic, it is important that you know about dot product and force.
The definition of work in science is different from the definition every other person is familiar with. It means much more than simple office work, school work, and house chores.
In this post, we will learn “What is work?” in science. And we will also learn how to find work done using its formula which is our main topic.
What is Work done?
When a body moves some distance due to some force, work is done. In this process, energy is converted from one form to another.
A scientific Definition of work done is:
“The work done on a system by a constant force is the dot product of the force and the distance through which the force acts.”
Note that the term used in physics is “Work done”. This is because it refers to a movement or motion that has taken place or is in process. It is different from work that means job or chores.
Key ingredients of work:
Moving on, there are three ingredients that are absolutely necessary to be kept in view while finding the work done. These three things are:
- Force
- Cause
- Displacement
It might have been obvious but there was still a need to mention these points. Why are these important? Read further to know.
The first one is force. You should know the horizontal component of the force. If not then it is important that you know about the mass and the acceleration of the body. Then you can calculate force using the force calculator.
Next, this force must be the Cause of the displacement we are finding the work for. If the force is applied perpendicular to the object then according to the dot product rule, no work should be done.
But if the body has still covered some displacement then the perpendicular force is not the cause. There must be some other force. Hence, the force we use must be the reason for displacement.
Q: Why do we use the dot product to find the work done? The dot product is used in the work done because we need ‘that’ component of the force that is acting in the direction of motion. (i.e F cos θ). The cross-product will not help us in this case as it uses the vertical component of force which is normal to the plane. It is not the cause. |
Work done formula
As the definition explained, work is the dot product of force and displacement. The formula of work is;
Work done = |F||d| cos θ
While the angle ???? is of force. Work is a scalar quantity as the dot product always provides. Its SI unit is Joule (J) same as energy. One joule is defined as:
“When a force of one newton causes a body to move by one meter then the work done is one joule.”
Joule in terms of base quantities is represented as newton-meter (Nm) and its dimension is [ML2T-2].
Before we learn how to find the work done, let’s have a quick glance at the types of work done.
Types of Work done
There are three types of work done based on the angle of the force.
Positive work done
When the angle of force is smaller than 90 degrees then the work done is positive. It is because the value of cos < 90 is greater than 0 and less than 1.
Negative work done
When the angle of force is greater than 90, in those cases work is said to be negative. The value of cos > 90 is less than 0 and greater than -1.
Zero work done
Lastly, when the value of force angle is exactly 90, the work done is zero. It is also called the minimum work done. Because cos 90 = 0.
There is also a term, maximum work done. It is when the force and displacement are perfectly parallel and the angle between them is zero. The value of cos 0 = 1 and is the maximum value of cos.
How to find the work done?
Now on to the main topic of the article. You will learn through different examples.
Example 1:
What will be the value of work done when the force is 80N at the angle of 45 degrees. The displacement is 20m.
Solution:
Step 1: Identify the value.
Force = 80N
Angle = 45
Displacement = 20m
Step 2: Use the values in the formula.
F.D = |F||d| cos θ
= (80)(20) cos (45)
= 1,131.4 J
Example 2:
What is the formula to find the work for a force parallel to displacement? Find Its value for the following data:
Force = 10N
Displacement = 5 m
Answer:
The formula for work done when force and displacement are parallel can be derived as follows.
Since the angle between both quantities is 0, hence:
Work = |F||d| cos θ
Work = |F||d| cos (0)
Work = |F||d| the value of cos (0) = 1
Work = F.d
It is the maximum work done. You can use the work calculator to find its value.
Now, on to the solution. Firstly, identify the values.
Force = 10 N
Displacement = 5 m
Now use these values in the derived formula.
Work = F.d
Work = (10)(5)
Work = 50 J
Example 3:
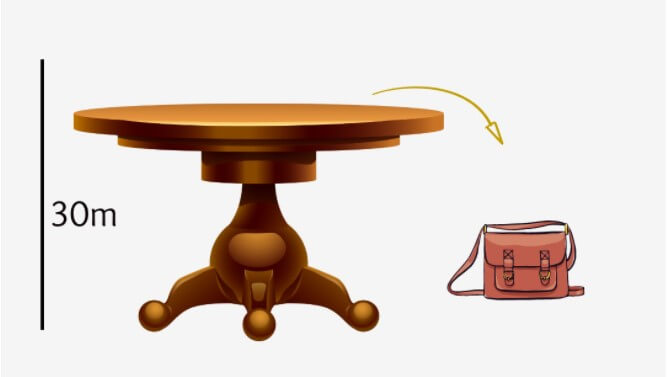
A bag of mass 4 kg fell from a table of height 30m. Calculate the work done.
Solution:
The given data is:
Mass = 4kg
Height = Displacement = 30m
Gravity = 9.8ms-2
Also, the object is falling in the direction of force (gravitational), which means both are parallel.
First, we need to find the force. In our case force is weight. (neglecting the air resistance)
F = ma
F = mg
F = (4)(9.8)
F = 39.2 N
Now, use it in the formula.
Work = F.d
Work = (39.2)(30)
Work = 1176 J
Example 4:
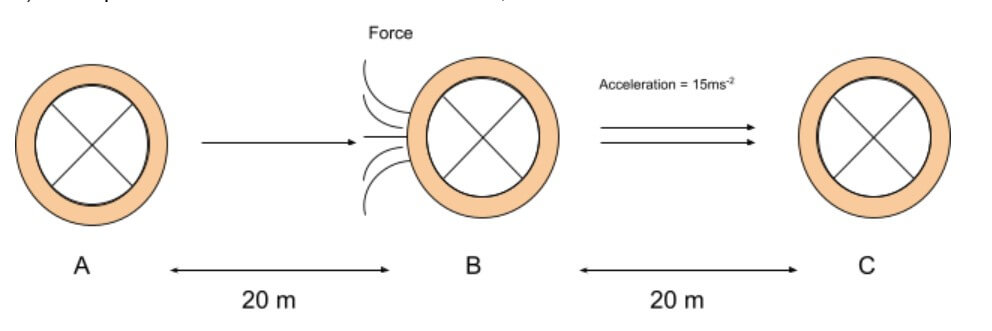
An object of 400 grams starts moving at a constant speed from point A. When it covers 20m (point b), a force is applied to it in the direction of motion.
It accelerates at a rate of 15ms-2 and reaches at a distance of 40 meters (point c) from point A. Find the work done. Also, the force of friction is 1.1N.
Solution:
Step 1: Write the given data.
Mass = 400 g = 0.4 kg
Acceleration = 15 ms-2
Displacement = From B to Point C = 40 - 20 = 20m
Force of friction = 1.1N
There are two forces involved. You can either calculate work done for each force separately or you can find the net force and use it in the work done formula.
We will use the former method.
Step 2: Find the force applied to the body.
F = ma
F = (0.4)(15ms-2)
F = 6 N
Step 3: Find the work done by the calculated force.
WorkF = |F||D| cos θ
WorkF = (6)(20) cos (0) (Angle is zero because F and d are parallel)
WorkF = 120 J
Step 4: Find the work done by friction.
Workfri = |F||D| cos θ
Workfri = (1.1)(20) cos 180 (Angle is 180 as friction opposes the motion)
Workfri = -22 J
Step 5: Calculate the net work done.
Worknet = WF + Wfri
Worknet = (120 J) + (-22 J)
Worknet = 98 J