Arc Length Calculator

The length of an arc calculator finds the total distance of an arc for any circle. You can find the arc length in both radians and degrees with this calculator. 

This calculator can find four geometrical measurements in two different units.

1. Sector area 
2. Arc length
3. Chord
4. Diameter

What is the arc length?

Arc length is the measurement of the distance between the endpoints of an arc along the circumference. An arc is always curved and this is what separates it from a chord which is the straight line joining the endpoints of an arc.

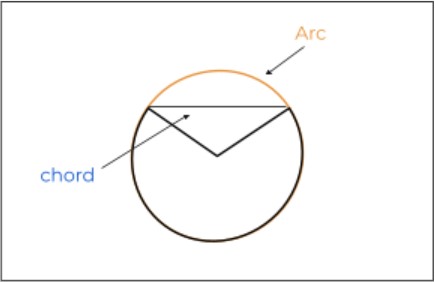
The image above is of a sector of a circle. An arc is not specified to a circle only. But in order to calculate its length, you have to know the radius of the circle that would be drawn by continuing the arc.

Arc length formula

The arc length is calculated using this formula:

Arc (L) = θr

Where theta θ is the central angle in radians and r is the radius. If you have the central angle in the degrees, then:

Arc (L) = (θ/180) x πr

This formula is derived from the fact that the proportion between angle and arc length remains the same. Keeping in mind a full circle, we can write:

L / θ = C / 2π

Where C is the circumference (length of an arc) and 2π is the central angle of the full circle. We can replace C with 2πr i.e value of the circumference in radians.

L / θ = 2πr / 2π

L / θ = r 

L = r * θ 

How to find the arc length of a circle?

Arc length can be calculated using a number of methods depending on the given data but the most suitable one is using the tool above. Because it provides you with other circle-related measurements without much effort.

To compute arc length, follow these instructions.

1. Measure or calculate the central angle.
2. Find the radius using the formula: r = diameter/2
3. Put both values in the arc length formula and solve.

Some solved examples are given below to remove any further confusion.

Example 1 (Using radius and central angle):

Assume a circle of radius 10 m. A sector of the circle makes an angle of 40 degrees. Find the arc length of this sector.

Solution: 

Step 1: Identify the values:

Radius = 10 

Central angle = 40.

Step 2: Convert degrees to radians.

1 degree = 0.0175 radians

40 degrees = 40 x 0.0175 radians 

= 0.6981 radians

Step 3: Use the values in the formula.

L = r * θ

L = (10)(0.6981)

L = 6.981 m

Example 2 (using radius and sector area):

If you have a circle of 6m radius which has a sector of area 40m² then find its arc length?

Solution:

Step 1: Identify the values.

Radius = 6m

Sector area = 40m²

Step 2: Find the central angle through the sector area.

Use the sector of an area formula and rearrange it in a way that will give you the value of the central angle. The formula is: 

Sector area (A) = ½ θr²

Rearranging:

θ = (A* 2) / r²

θ = (40* 2) / 6² 

θ = (80) / 36 

θ = 2.22 

Step 3: Use the values in the formula.

L = r * θ

L = 2.22 * 6

L = 13.333

This is the final answer. Similarly, if you are given the sector area and the central angle, you can use the sector area formula to find the radius. Then you can follow the same method as the given examples.