To calculate result you have to disable your ad blocker first.
Proportion Calculator
Enter the 3 input values, the 4th input should be unknown (x), and hit the calculate button to find the proportion between two fractions using this proportion calculator.
Table of Contents:
Proportion Calculator
Solve the value of an unknown variable using this proportion calculator. It is an online tool that assists you in solving the proportions without much effort. This proportion solver makes the process of solving proportions quite effortless.
You only have to put the values and a variable X in the given boxes to get the value of X.
What is the proportion?
A proportion represents the relationship between two quantities. It consists of two ratios of two fractions joined by an equal sign “=”. A proportion can be written as:
2 : 5 = 7 : 4 or
2/5 = 7/4
Wikipedia defines proportion as,
“In mathematics, two varying quantities are said to be in a relation of proportionality, if they are multiplicatively connected to a constant; that is when either their ratio or their product yields a constant. The value of this constant is called the coefficient of proportionality or proportionality constant.”
There are mainly three types of proportions.
Direct proportion:
If the quantity of one variable increases, the quantity of another variable also increases, and vice versa. It is known as a direct proportion.
Inverse proportion:
If the quantity of one variable increases, the quantity of another variable decreases, and vice versa. It is known as the inverse proportion.
Compound proportion:
It is a type of proportion that deals with two or more quantities at a time. I.e. 2 : 3 : 4 = 3 : 7 : 1
How to solve a proportion?
Students have to solve proportions by hand in their exams and classrooms. This tool can be very helpful to quickly complete the assignments and homework. Moreover, it can be used to learn the calculations of proportion. Here, we will illustrate how to calculate proportion by yourself.
Cross multiplication method
To calculate a missing value or unknown variable in a proportion, follow the below steps:
- Write the given values in fraction form. Use any variable to represent the unknown value.
- Join both fractions using an equal sign.
- Multiply both fractions diagonally. I.e. multiply the numerator of the first fraction with the denominator of the second fraction and multiply the numerator of the second fraction with the denominator of the first fraction.
- Write both numbers after multiplication and put an equal sign between them.
- Find the value of the variable by isolating it on either side of the equation.
Example – Direct proportion
A train from Seoul to Busan travels 300 km distance in 4 hours. How much time will it take to reach a distance of 500 km?
Solution:
Step 1: Write the given values in fraction form. Use any variable to represent the unknown value.
It travels 300 km in 4 hours, the ratio will be: 300 / 4
The ratio for the distance of 500 km will be: 500 / X
Step 2: Join both fractions using an equal sign.
300 / 4 = 500 / X
Or
300 : 4 = 500 : X
Step 3: Multiply both fractions diagonally. I.e. multiply the numerator of the first fraction with the denominator of the second fraction and multiply the numerator of the second fraction with the denominator of the first fraction.
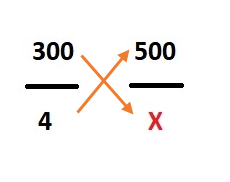
Step 4: Write both numbers after multiplication and put an equal sign between them.
300 X = 500 × 4
Step 5: Find the value of the variable by isolating it on either side of the equation.
X = 2000 / 300
X = 6.6 hours approx.
So, the train will take approximately 6 and a half hours to cover a distance of 500 km.
Example – Inverse proportion
In a toy manufacturing factory, 3 workers make a box of toys in 8 days. The company has hired 2 more workers to increase the production of the unit. There are a total of 5 workers in the factory now. How long will it take to complete that same task by 5 workers?
Solution:
Step 1: Write the given values in fraction form. Use any variable to represent the unknown value.
Ratio of workers before and after = 3 / 5
Ratio of days of completion = X / 8
Step 2: Join both fractions using an equal sign.
3 / 5 = X / 8
Step 3: Multiply both fractions diagonally. I.e. multiply the numerator of the first fraction with the denominator of the second fraction and multiply the numerator of the second fraction with the denominator of the first fraction.
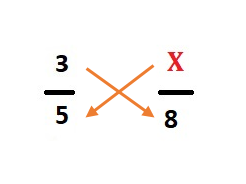
Step 4: Write both numbers after multiplication and put an equal sign between them.
5 X = 3 × 8
Step 5: Find the value of the variable by isolating it on either side of the equation.
X = 24 / 5
X = 4.8
So, 5 workers will manufacture the toys in approx. 4.8 days.
FAQs
How do you calculate proportion?
Proportion can be calculated by using a cross-multiplication method. In the cross-multiplication method, we diagonally multiply the numerator and denominator of both fractions and calculate the value of an unknown variable by isolating it on one side of the equation.
For example, we have two fractions as:
2/3 = 4/x
By cross multiplication, we get:
2x = 12 è x = 6
What are examples of proportions?
The following are some examples of proportions:
- We use proportions of ingredients for cooking a specific amount of food.
- We compare the prices of various shopping centers by using proportions.
- Builders mix sand and cement into the gravel to make a solution by using specific proportions.
- Chemists make several chemical formulas and medicines by using proportions of various chemicals and drugs.
- A rope of specific weight and length. The length and weight of the rope are proportional.
- The sizes of the shapes of any objects can be proportional to each other.
What is the ratio of 4 to 3?
The ratio of 4 to 3 can be written as 4 : 3. It means that the second quantity is 1/3 of the first quantity.
A few equivalent ratios of 4 : 3 are:
| 4 : 3 | 8 : 6 | 12 : 9 | 16 : 12 | 20 : 15 |
| 24 : 18 | 28 : 21 | 32 : 24 | 36 : 27 | 40 : 30 |
| 44 : 33 | 48 : 36 | 52 : 39 | 56 : 42 | 60 : 45 |
| 64 : 48 | 68 : 51 | 72 : 54 | 76 : 57 | 80 : 60 |
| 84 : 63 | 88 : 66 | 92 : 69 | 96 : 72 | 100 : 75 |
What is the ratio of 1 to 5?
A ratio of 1 to 5 can be written as 1 : 5. It shows that the quantity in second place is five-time the quantity in the first place. Some equivalent ratios of 1 : 5 are:
| 1 : 5 | 2 : 10 | 3 : 15 | 4 : 20 | 5 : 25 |
| 6 : 30 | 7 : 35 | 8 : 40 | 9 : 45 | 10 : 50 |
| 11 : 55 | 12 : 60 | 13 : 65 | 14 : 70 | 15 : 75 |
| 16 : 80 | 17 : 85 | 18 : 90 | 19 : 95 | 20 : 100 |
| 21 : 105 | 22 : 110 | 23 : 115 | 24 : 120 | 25 : 125 |