Modulo Calculator

Welcome to the modulo calculator! The most accurate online tool to calculate the modulo operations. The modular calculator only takes dividend and divisor from the user to calculate the remainder after the division.

Interested in modulo operations? We are going to discuss modulo definition, how to find mod using a dividend and divisor, how to use modulus calculator, modulo arithmetic operations and much more in this space.

How to use modulo calculator?

The mod calculator by meracalculator offers quite a simple interface. It lets you calculate the mod by taking dividend (a) and divisor (b) as input. To calculate modulo using inverse modulo calculator, follow the below steps:

• Enter the dividend in the given input box.
• Enter the divisor in the next input box.
• Use the Calculate button to get the remainder.
• Use the Reset button to enter the new values.

Did you find what you were looking for? If not, stay with us because we are going to explain modulo and its calculation in the next section.

Modulo definition – What is modulo?

Modular arithmetic is a calculation that involves a number that is reset to zero any time a whole number greater than 1, namely mod is obtained. The calculation is also called clock arithmetic.

The automated 24-hour clock resets to 0 at midnight is an example of modulo.

In mathematics, if we divide a number by another number, the number after division or the remainder is called modulo. The short form ‘mod’ is used to refer modulo in general. It is also represented by the percentage sign %.

The standard format of mod can be written as:
a mod n
Where:

a is the dividend, and

n is the divisor.

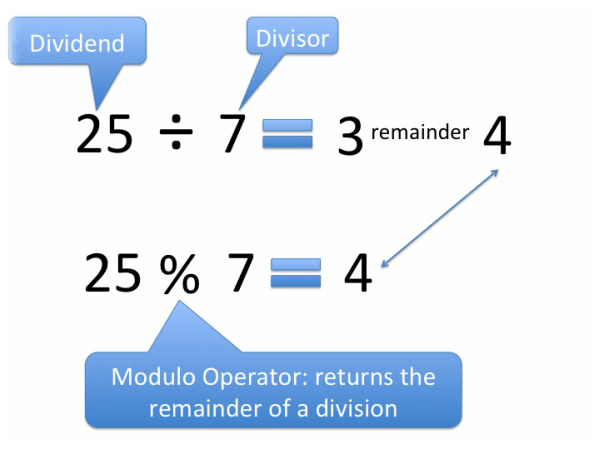
Let’s find out how you can calculate the mod operation in exams.

How to calculate modulo?

Modulo can be calculated by dividing two numbers. One number being nominator and one being denominator, these both numbers are also referred as dividend and divisor. Follow these steps to calculate the modulo of two numbers:

• Write down the dividend (a) and divisor (b).
• Divide the dividend with divisor using integer division.
• Write down the answer and separate the integer and decimal part.
• Multiply the integer part of the answer with the divisor (b).
• Calculate the difference between the dividend (a) and the number you got in the previous step after multiplication.
• The occurring difference is the modulo or remainder.

Let’s use an example to further understand the calculation.

Example:

Let’s calculate 10 mod 3 by following above steps:

Step 1: Write down the dividend (a) and divisor (b).

a = 10, b = 3

Step 2: Divide the dividend with divisor using integer division.

a/b = 10/3 = 3.33

Step 3: Write down the answer and separate the integer and decimal part.

Integer part = 3, Decimal part = 0.33

Step 4: Multiply the integer part of the answer with the divisor (b).

3 × 3 = 9

Step 5: Calculate the difference between the dividend (a) and the number you got in the previous step after multiplication.

Dividend = 10

So, 10 – 9 = 1

The modulo for 10 mod 3 is 1.

Modulo arithmetic operations

Modular arithmetic is, in general, an arithmetic system for integer, where a certain number is packed up by other numbers. We can represent the modulo operations in several ways.

• A mod C = B mod C
• A ≡ B (mod C)
• A = B + K * C
• C | (A - B)

We can also carry out modulo calculations. Followings are the calculations on modulo operations.

1. Modular addition and subtraction

The modular addition and subtraction can be performed as:

(A + B) mod C = (A mod C + B mod C) mod C

(A - B) mod C = (A mod C - B mod C) mod C

The above expression can be concluded as:

If we take the modulo of sum of two numbers, it will be equal to the sum of modulo calculated individually for both numbers, and then multiplied by the divisor.

The first step is taken to remove the quotient component and the mod process is re-used. It can be demonstrated with an example:

A = 13, B = 6, C = 2

(13 + 6) mod 2 = (13 mod 2 + 6 mod 2) mod 2

Left side of the equation: (13 + 6) mod 2 = 19 mod 2 = 1

Right side of the equation: (13 mod 2 + 6 mod 2) mod 2 = (1 + 0) mod 2 = 1 mod 2 = 1

The equations for subtraction are the same.

2. Modular multiplication

The equation for modular multiplication can be stated as:

(A × B) mod C = (A mod C × B mod C) mod C

This equation can help in the handling of large numbers, and we do not immediately know modulo of the great numbers.

Let’s use an example again to demonstrate the modular multiplication using above equation. Suppose we have the following values:

 A = 12, B = 7, C = 3

(12 × 7) mod 3 = (12 mod 3 × 7 mod 3) mod 3

Left side of the equation: (12 × 7) mod 3 = 84 mod 3 = 0

Right side of the equation: (12 mod 3 × 7 mod 3) mod 3 = (0 × 1) mod 3 = 0 mod 3 = 0

3. Modular exponentiation

The equation for modular multiplication can be stated as:

A^B mod C = ((A mod C) ^B) mod C

For large numbers, this equation of modular exponentiation is even more helpful. Here is the example of modular exponentiation:

Suppose, we have the same values as in previous example.

A = 12, B = 7, C = 3

(12 ^ 7) mod 3 = ((12 mod 3) ^7) mod 3

Left side of the exponentiation equation: (12 ^ 7) mod 3 = 35831808 mod 3 = 0

Right side of the exponentiation equation: ((12 mod 3) ^7) mod 3 = (0^7) mod 3 = 0 mod 3 = 0.

In this case, it may not be so obvious how useful this formula is, as the calculator must still be used to find the result of exponentiation. You can use our exponent calculator to calculate the exponent for above example. Moreover, our modular arithmetic calculator above makes this process much easier than ever.

The multiplication property mentioned above can be very helpful when dealing with the big numbers. Here is an example of modulo operation with multiplication property using some large numbers.

2^100 = 2^50 × 2^50

2^100 mod 3 = (2^50 mod 3 × 2^50 mod 3) mod 3

2^100 mod 3 = (1 × 1) mod 3 = 1

How do you calculate 15 mod 26?

You can calculate the 15 mod 26 by following the steps below:

• Identify the dividend and

Dividend = 15, Divisor = 26

• Divide the dividend with divisor using integer division.

15/26 = 0.57

• Write down the answer and separate the integer and decimal part.

Integer = 0, Decimal = 0.57

• Multiply the integer part of the answer with the divisor.

0 × 26 = 0

• Calculate the difference between the dividend and the number you got in the previous step after multiplication.

15 – 0 = 15

15 is the modulo for 15 mod 26.

What is the precedence of modulo operation in math?

In mathematics, modulo (%) operation has the same precedence as of multiplication (×) and division (÷).

How do you calculate A % B?

Suppose we have:

A = 25, and B = 4

• Identify the dividend and

Dividend = 25, Divisor = 4

• Divide the dividend with divisor.

25/4 = 6.25

• Write down the answer and separate the integer and decimal part.

Integer = 6

• Multiply the integer part of the answer with the divisor.

6 × 4 = 24

• Calculate the difference between the dividend and the number you got in the previous step after multiplication.

25 – 24 = 1

So, 25 % 4 = 1.