Polynomial Factoring Calculator

Polynomial Factoring Calculator is a mathematical tool that helps to find possible factors of the long polynomial and plays an important role in solving long polynomials by using the factorization method.

It also provides a step-by-step solution to every problem and an explanation of how to apply the factorization method to long polynomials.

What is a polynomial?

In mathematics, a polynomial is an algebraic expression that is the combination of two or more terms and constants. In another way, say that it contains at least one variable and the sum/difference or multiple of two or more terms while not the difference of any terms.

In general, polynomial is the combination of two words “poly” and “nomial”. The “Poly” means “many” and “nomial” means “terms”. The polynomial can be represented by the “P(x)”. Due to the terms, there are three types of polynomials such as monomial, binomial, and trinomial.

A monomial is named due to one term, a Binomial is called due to the two terms, and a trinomial contains only the three terms. Moreover, especially due to only the zero term “p(x) = 0(x)” in the polynomial is named as the zero polynomial.

What is the Factoring method?

Factoring is the simple way to solve the different order polynomials by using different techniques of factorization. By factorization generate a pair of polynomials of less order than the original polynomial. Then the product of the pair returns to the original polynomial.

Methods to factorize the polynomial

There are different methods to determine the factor of the polynomials. Every method has its specialty and is used for a particular type of polynomials.

• Grouping method
• Greatest Common Factor (GCF)
• Difference of Squares
• By Factor Theorem
• Factorize using identities
• Factorize by quadratic Formula

How to factorize by Grouping method?

In this method, the polynomial terms factorize by making the group of the terms using the factorization and multiplication of the number. Follow the below steps to factorize the polynomial by grouping method.

• Firstly, multiply the constant term with the coefficient of the “x²” with its sign.
• Then find the pair of factors of the constant number.
• Then choose the suitable pair of factors to take the consideration on the sign of the “x” terms.
• Then distribute the polynomial into the pair of the two terms.
• After that determine the GCF (common factor) of the pairs and find the factors of the polynomial.

Example

Find the factor of the “x² - 5x + 6”.

Solution

Step 1: Find the multiple of the constant term and coefficient of the “x²” term.

x² - 5x + 6

• coefficient of “x²” = 1
• constant term = 6

Multiple of the terms = 6

Prime Factors of the “6” = 1× 2 × 3 × 6

Step 2: Distribute the polynomial as the sum of the “x” value that resultant is equal to the above term.

x² - 5x + 6 = x² -3x -2x + 6

Make the pair of terms and take the common factor from the pairs.

                  = x² -3x -2x + 6

                  = x (x -3) -2 (x – 3)

x2 - 5x + 6 = (x -3) (x – 2)

How to factorize polynomials by the Greatest Common Factor (GCF)?

In this method, determine the GCF of all terms and exclude the common term from all polynomial terms. Follow the below steps to determine the factor of the polynomial.

• Firstly, determine the GCF of all polynomial terms.
• Express each term as the multiple of the GCF if needed.
• Use the law of distribution to take common values from all terms.

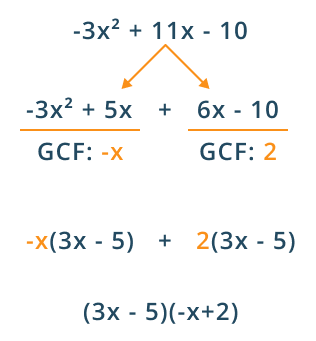
Example

Factorize the given polynomial “2x⁴-4x²+6x”.

Solution

Step 1: Find the greatest common factor of the given polynomial from all terms.

2x⁴-4x²+6x

We note that the “2x” is the highest common factor of all terms.

Step 2: Now take the GCF common from all terms.

2x⁴-4x²+6x = 2x (x³- 2x +3)

Thus, 2x (x3- 2x +3) is the factorization of the given polynomial.

How to factorize polynomials by Difference of Squares?

In this method, the expression is viewed in the form of the difference of the two perfect squares then it factorizes in the product of the factor by using the particular algebraic identity. Follow the below steps to determine the factor of the polynomial.

• Firstly, convert the term into the appropriate squares if needed.
• By using the square identity get the factor of the polynomials.

Square identity can be defined as, a² – b² = (a + b) (a - b).

Example

Factorize the polynomial if is given as “4x²-64”.

Solution

Step 1: First, convert into the difference of squares.

4x² - 64 = (2x)² – (8)²

Step 2: Using the square identity of polynomials get the factor of polynomials.

a² – b² = (a + b) (a - b)

Then the polynomial,

4x2 - 64 = (2x + 8) (2x -8)

How to factorize polynomials By Factor Theorem?

In this method, we put the random constant number in the given polynomial and solve the given expression if the resultant is zero then the provided number is a factor of the polynomial.  While the answer is either zero then the provided number is not the factor of the polynomial.

Start from the “1, 2, 3, and so on (positive or negative numbers)” at that time if the number of factors is not equal to the highest power of the polynomial. It mathematically can be defined as,

The term (x-a) is the factor of the polynomial if “P(a) = 0” then “a” is the factor of the polynomial and is also known as the rational zeros of the polynomial. Here, we provide a manual example to find the factor by factor-theorem.

Example

Find the factor of the polynomial if it is “x²-5x+6”.

Solution

Step 1: write the polynomial as equal to “P(x)”.

P(x) = x²-5x+6

Step 2: Put the random number to determine the factor of the polynomial.

Start from the “ 1, 2, 3, and so on” at that time if the number of factors is not equal to the highest power of the polynomial.

Check “1” is the factor of the given polynomials.

P(x) = x² - 5x + 6

P(1) = (1)² – 5 (1)+ 6

       = 1 - 5 + 6 = 2 ≠ 0

Thus, “1” is not the factor of the given polynomial.

Check “2” is the factor of the given polynomials.

P(2) = (2)² – 5 (2)+ 6

       = 4 - 10 + 6 = 0

Thus, “2” is the factor of the polynomial.

Step 3: Check “3” is the factor of the given polynomials.

P(2) = (3)² – 5 (3)+ 6

        = 9 - 15 + 6

        = 15 – 15 = 0

Thus, “3” is the factor of the polynomial.

Factor can be written as “(x-2) & (x-3)”.

Thus, polynomials can be written as,

x2 - 5x + 6 = (x - 2) (x-3)