To calculate result you have to disable your ad blocker first.
Standard Error Calculator
Select a data type(Raw or Summary), enter values in the input box for respective selection & hit the calculate button to find standard error (SE) by using standard error of the mean calculator.
Table of Contents:
Standard Error Calculator
Standard error calculator is used to calculate the standard error of the mean of a set of numbers. This sem calculator provides the option to enter raw data & summary data and calculates the SE values by using a standard error formula with a detailed step-by-step solution.
In raw data selection, our standard error of the mean calculator finds the necessary values for the calculation of standard error such as: sample standard deviation, sum of the squares, and mean.
What is Standard Error?
The standard error tells us how data values are far or close to the mean of a sample from the population mean. In other words, “the dispersion of the sample mean”.
The standard error is kind of a reliability check, to know how much the sample mean can be trusted. It is used in the fields of medicine, engineering, and many more.
Standard Error Formula
The formula of standard Error includes standard deviation and sample size. SE formula is mathematically written as;
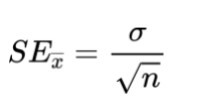
Where the sigma symbol in the numerator represents the standard deviation and the n in the denominator represents the sample size of data.
How to Calculate Standard Error?
The method of finding standard error depends on the data available. If one has raw data, one will first have to count the sample values, find the standard deviation, and use these values in the standard error formula.
On the other hand, if you already have the summary data, simply plug in the value in the SE formula written above. You can double-check your answer from the standard error of the mean calculator.
Keep reading to learn more about how to calculate standard error by the below separate examples of raw data and summary data.
Example:
What is the standard error of the following Raw data?
1, 23, 4, 12, 10, 31.
Solution:
Step 1: Count the values.
N = 6
Step 2: Find the standard deviation.
The formula is:
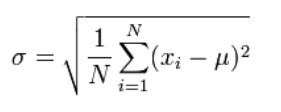
Mean = (1, 23, 4, 12, 10, 31) / 6
= 81 / 6
= 13.5
Sum of the squares = (1-13.5)2 + (23-13.5)2 + (4-13.5)2 + (12-13.5)2 + (10-13.5)2 + (31-13.5)2
= 657.5
Putting the values in the formula
=(657.5 / 6)½
= 10.47
Step 3: Use this data in the standard error formula.
= 10.47/√6
= 4.274
Example 2:
Find the standard error of given summary data, if the variance of the sample data is 234 and the sample count is 7.
Solution:
Step 1: Write the given data.
Variance = 234
Count (N)= 7
Step 2: Find the standard deviation.
= Variance /N-1
= 234 / 7-1
= 234 / 6
= 39
Step 3: Use the standard error formula.
= 39 / √6
= 15.9