Standard Deviation Calculator

Standard Deviation Calculator

SD calculator is used for calculating the standard deviation and the other values required to calculate the standard deviation. These values include:

• Variance 
• Count
• Number of samples
• Sum of squares

You can use this standard deviation calculator to find the standard deviation for both sample and population. 

What is the standard deviation?

“The standard deviation is a measure of the amount of variation or dispersion of a set of values”

If the values in a data set are close to each other e.g 2,3,4, then the value of standard deviation is small. On the contrary, when the values have greater differences e.g 1,18,90, then the value of standard deviation is high. 

Standard deviation formula:

The formula of standard deviation is very much the same as that of the variance.

For Population: 

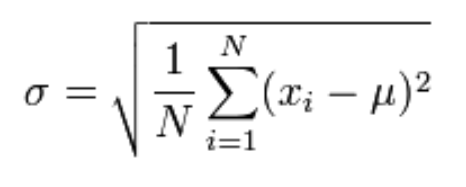
For sample: 

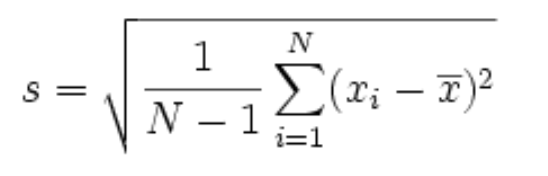
Where 

• σ,s = Standard deviation 
• µ, x̅ = Mean 
• x_i = Individual values
• N = Count

Population mean formula:

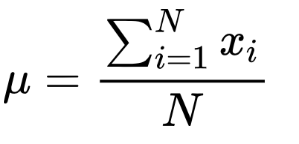
Sample mean formula:

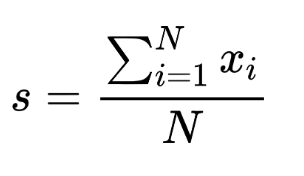
How to find the standard deviation?

Calculation of standard deviation comprises many steps and it will be tiring when the data set contains a large number of values. The best option is to use the standard deviation calculator above.

But for those who want to learn the manual process, below is an example that will explain all calculations.

Example:

For the following set of data find the standard deviation.

1,3,5,7,9,11,13,15

Solution: 

Step 1: Count the values.

N = 8

Step 2: Find the mean of the sample.

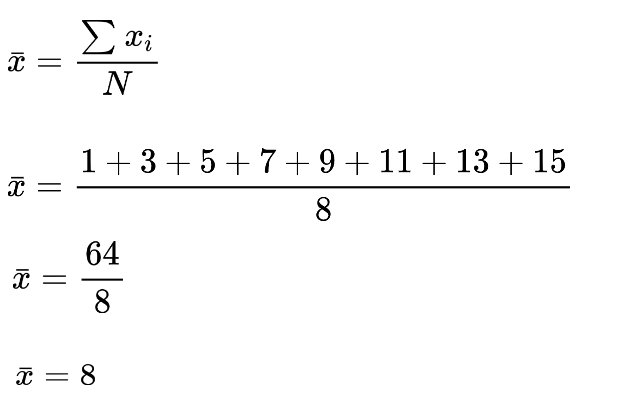
Step 3: Find the square of the difference of values from the mean.

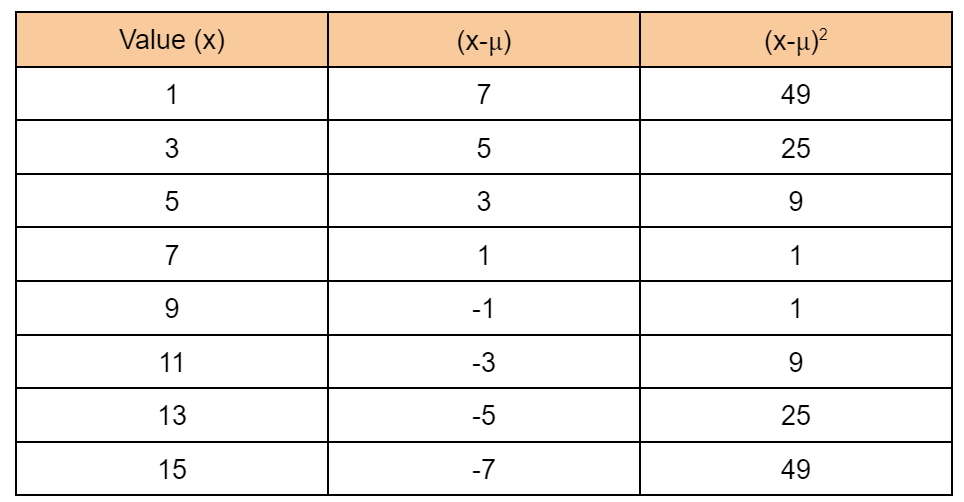
Step 4: Find the sum of (x-µ)².

= Σ(x-µ)²

= 49+25+9+1+1+9+25+49

= 168  

Step 5: Calculate variance.

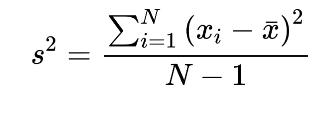
= 168/8-1

= 168/7

= 24

Step 6: Take the square root of the variance to find the standard deviation.

s = (24)^1/2

s = 4.89

References

• Standard deviation. Wikipedia.
• Standard Deviation Calculator - Sample/Population.