To calculate result you have to disable your ad blocker first.
Variance Calculator
To find the value of variance, Enter the values of the sample or population in the variance calculator.
Table of Contents:
Variance Calculator
This variance calculator can compute the variance, a measure of dispersion. You can calculate the variance of a small group (sample) or the entire population. This variance calculator with steps also calculates the standard deviation, sum of squares, and mean of the given data set.
What is the variance?
In statistics, variance is a measurement of the spread of readings or values from the mean of the whole data set.
Variance is used in business by investors to measure profit.
Variance formula:
The formula used to calculate population variance is:
(/sigma \^{\2\}\=\\frac{\1\}{\N\}\\sum _{i=1}^N\\left(X_i-\\mu \right)^2/)In this equation, N is the size of population and is the population mean.
To find sample variance, the equation used is:
-- { s }^{ 2 } = \\small \\dfrac{1}{n-1} \\large\\displaystyle\\sum_{ i = 1 }^{ N } { \\left( { X }_{ i } - \\bar{X} \\right) }^{ 2 }In this equation, n is the size of the sample, and x bar represents the sample mean.
Difference between Population and sample:
In statistics, population means the number of things, not necessarily people.
The main difference between population and sample is the size of the group. Population refers to the entire group while sample means a portion of the group.
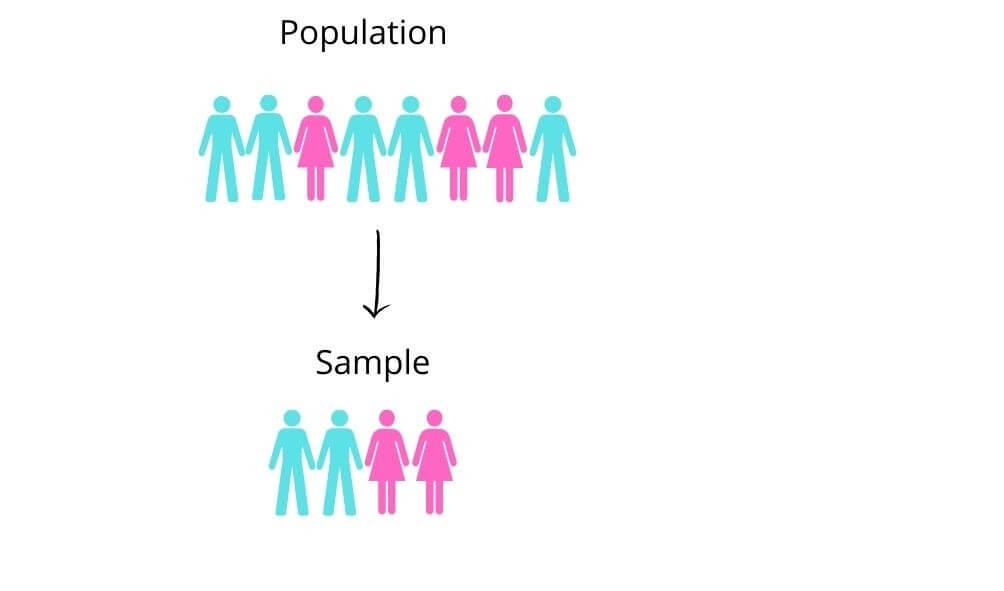
Usually, the sample is used in calculations.
How to find variance?
Example:
A student measured the diameter of a ball through a vernier caliper five times. The set of data obtained is as follows.
1st | 2nd | 3rd | 4th | 5th |
2mm | 2.5mm | 3mm | 2.4mm | 2.5mm |
Find the variance of this group.
Solution:
Step 1: Arrange the values in ascending order.
2, 2.4, 2.5, 2.5, 3
Step 2: Find mean.
Mean = ∑ x / n
= 2 + 2.4 + 2.5 + 2.5 + 3 / 5
= 2.48
Step 3: Identify values:
Mean = 2.48
Number if values = 5
Step 4: Find the square of values subtracted from the mean.
Value (x) | (x-μ) | (x-μ)2 |
2 | 0.48 | 0.2304 |
2.4 | 0.08 | 0.0064 |
2.5 | -0.02 | 0.0004 |
2.5 | -0.02 | 0.0004 |
3 | -0.52 | 0.2704 |
(Note: the square of (x-) neutralizes the value i.e no +ve or -ve sign.)
Step 5: find ∑(x- μ)2.
= 0.508
Step 6: Put in the formula:
-- { \\sigma }^{ 2 } = \\dfrac{ 1 }{ N } \\displaystyle\\sum_{ i = 1 }^{ N } { \\left( { X }_{ i } - \\mu \\right) }^{ 2 }-- { \\sigma }^{ 2 } = \\dfrac{ 1 }{ 5 }\times0.508
σ2 =15 X 0.508
= 0.1016