To calculate result you have to disable your ad blocker first.
Triangular Pyramid Surface Area Calculator
Select what you want to calculate and place the values in the given input boxes to find the surface area of a regular pyramid or any other quantities related to a pyramid.
Table of Contents:
Triangular Pyramid Surface Area Calculator
The surface area of triangular pyramid calculator handles all pyramid related calculations like a pro. It doesn’t matter if you want to find the surface area, volume, base area, base width, or base length. It offers a one-stop-shop for all calculations of a pyramid.
What is a pyramid?
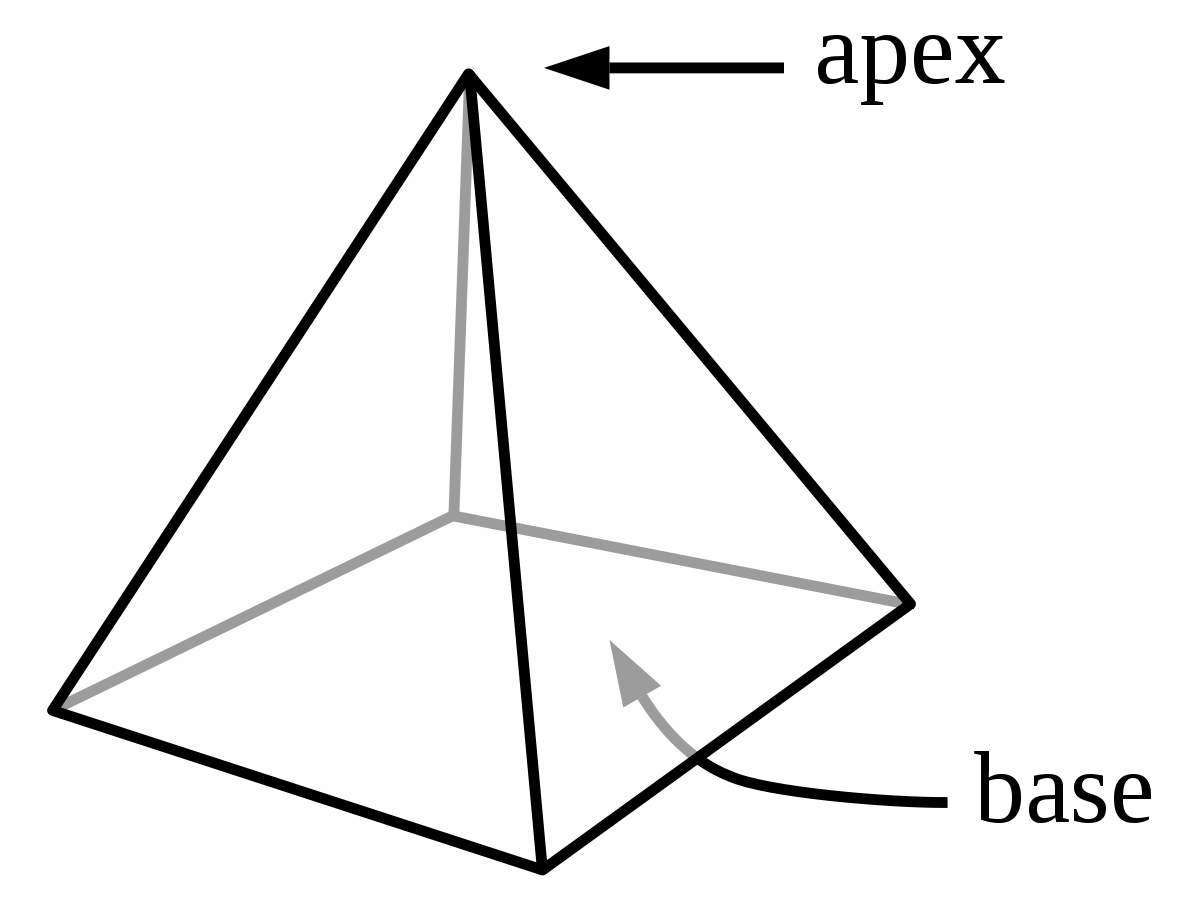
A pyramid is a solid object having a polygon base and triangular sides that meet at the top. A pyramid is a three-dimensional structure and a polyhedron.
Formula
The pyramid area calculator automatically utilizes the relevant formula and calculates the area, volume, base, and other terms accordingly.
It composes the required formula in the run time after gathering the values and that is why it is safe to say that it is also a surface area of a triangular pyramid formula calculator.
Triangular Pyramid
Area of the base (A) = ½ * a * s
Surface Area of Pyramid = A + ((3/2) sl)
Volume of Pyramid = (1/6) abh
Where,
- a = apothem length
- s = side length
- sl = slant height of a pyramid
- abh = area of base * height
In case you don’t want to get stuck in equations, a pyramid volume calculator can ease your calculations of a pyramid.
Square based pyramid
Area of the base (A) = [s²]
Surface Area of square Pyramid = [s² + 2sl]
Volume of Square Pyramid = [(1/3)b²h ]
The above equation can be used to calculate the square pyramid volume.
Where,
- s = side length
- sl = slant height
- b = base
- h = height
Pentagonal
Area of Base : [(5/2)as]
Surface Area of Pyramid : [(5/2)as + (5/2)sl]
Volume of Pyramid : [ (5/6)abh]
Where,
- As = area of side length
- sl= slant height
- abh = area of base * height
Hexagonal based pyramid
Area of Base: [(6/2) as]
Surface Area of Pyramid: [3as + 3sl]
Volume of Pyramid: [abh]
Where,
- As = area of side length
- sl= slant height
- abh = area of base * height
A pyramid is a polyhedron with one face as a base, a polygon, and all the other faces of triangles meeting at a common polygon vertex as the apex. It is a structure where the upper surfaces are triangular and converge on one point.
Surface area of a triangular pyramid calculator
Wondering how to find the surface area of a pyramid? Let’s find it step by step in this section.
Find the area, surface area, and volume of a triangular pyramid with the given apothem length 2, side 3, height 4, and the slant height 5.
Step 1: Find the area of the base.
Area of the base (A) = ½ * a * s = 0.5 * 2 * 3 = 3.
Step 2: Find the surface area of the pyramid.
Surface Area of Pyramid = A + ((3/2) sl) = 3 + ((3/2) * 3 * 5) = 3 + (1.5 * 15) = 3 + 22.5
= 25.5.
Step 3: Find the volume of a pyramid.
Volume of Pyramid = (1/6) abh = (1/6) * 2 * 3 * 4 = 0.17 * 24 = 4.08.
Find the area, surface area, and volume of a right square (right rectangular) pyramid with the given side length 3, height 4, and slant height 5.
Step 1: Find the area of the base. (Right square pyramid calc: find a)
Area of the base (A) [s²] = 32 = 9
Step 2: Find the surface area of the pyramid.
Surface Area of Pyramid = [s² + 2sl] = 32 +2*5= 9+10 = 9 +2*5*3 =9+30 = 39
Step 3: Find the volume of a pyramid. (Right rectangular pyramid calc: find v)
Volume of Pyramid = [(1/3) b²h] = [(1/3)*92 *4] = (1/3)*9*4 = 36/3 = 12
Step 4: Find the lateral area of the pyramid. (Right rectangular pyramid calc: find a_l)
Lateral area of rectangular pyramid:
AL = l√((w/2)2 + h2)+ w √((l/2)2 + h2)
AL = 3√((3/2)2 + 42) + 3√((3/2)2 + 42)
AL = 3√(73/4) + 3√(73/4)
AL = 12.82 + 12.82 = 25.64
Find the area, surface area, and volume of a Pentagonal pyramid with the given side apothem length 2, side 3, Slant height 4, and height 5.
Step 1: Find the area of the base.
Area of Base : [(5/2)as] = [ (5/2)2*3]= 5/2*6= 2.5*6= 15
Find the surface area of the pyramid.
Surface Area of Pyramid : [ (5/2)as + (5/2)sl ]= 15+(2.5*3*4) = 15+ (2.5*12) =15+30 = 45
Find the volume of a pyramid.
Volume of Pyramid : [(5/6)abh] = (5/6) 2*3*5= (5/6) * 30 = 0.833 *30 = 25
Find the area, surface area, and volume of a Hexagonal pyramid with the given side apothem length 2, side 3, Slant height 4, and height 5.
Step 1: Find the area of the base. Area of Base: [(6/2) as] = [(6/2) 2*3= (6/2) *6 = 3*6 = 18
Find the surface area of a pyramid.
Surface Area of Pyramid: [3as + 3sl] = [(3*2*3) + (3*3*4)] = 18+36 = 54
Find the volume of a pyramid.
Volume of Pyramid: [abh] = 2*3*5 = 30
FAQs
How to find the surface area of a square pyramid?
The surface area of the squared pyramid can be found using the below equation:
A = a (a + √ (a2 + 4h2))
Where a represents the side length, and h is the pyramid's height.
How do you find the total surface area of a pyramid?
The total surface area of the pyramid can be calculated using the below formula:
T.S.A = (1/2)pl + B
Where l is the slant height, B is the base area, and p represents the perimeter of the base.