Asymptote Calculator

Find asymptotes for any rational expression using this calculator. This tool works as a vertical, horizontal, and oblique/slant asymptote calculator. 

You can find the asymptote values with step-by-step solutions and their plotted graphs as well. Try using some example questions also to remove any ambiguity. 

How to use asymptote calculator?

Follow the instructions below to operate this calculator.

1. Enter the rational expression carefully.
2. Confirm the expression from the display box.
3. Lastly, click on the calculate option.

Reset as many times as you want. The first result displayed is of horizontal asymptote but you can click on “Show Steps” for vertical and oblique asymptote along with the graph.

Now, let’s see how you define asymptotes, what are its types, and some other related topics. 

What are asymptotes?

Asymptote definition is:

“Such a line that is approached by a curve but does not meet the curve. Or meets the line as the curve approaches infinity.”

Sounds like limits right!?

Types:

There are three types of asymptotes:

• In Horizontal asymptotes, the line approaches some value when the value of the curve nears infinity (both positive and negative). lim_x→±∞ f(x) = L

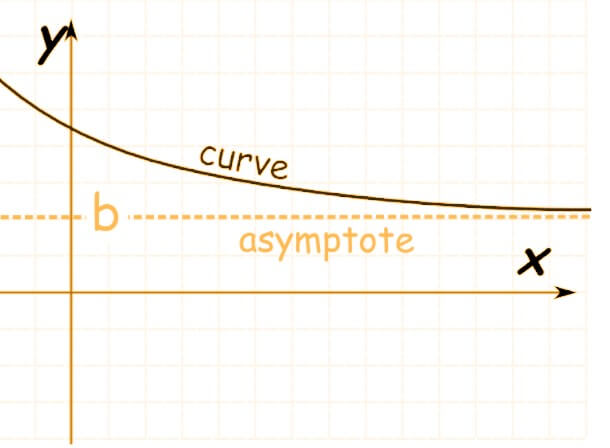
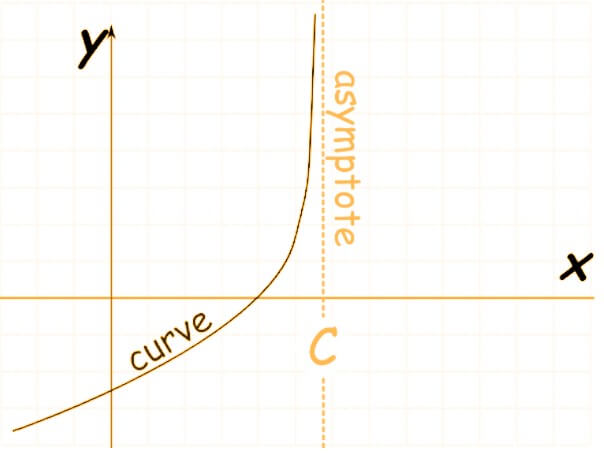
• Vertical asymptote occurs when the line is approaching infinity as the function nears some constant value. lim_x→l f(x) = ∞

• It is a Slant asymptote when the line is curved and it approaches a linear function with some defined slope. 

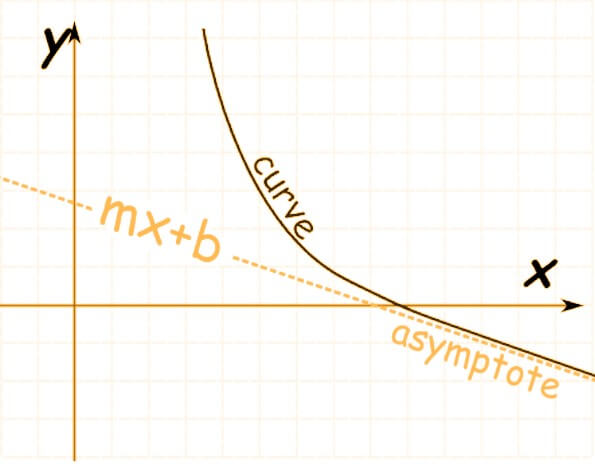
How to find Asymptotes?

Now the main question arises, how to find the vertical, horizontal, or slant asymptotes. Besides using the asymptotes finder, you can learn some rules and techniques to figure them out yourself. 

Let’s go into the details one by one.

Horizontal asymptotes:

There are three possibilities regarding horizontal asymptotes for a particular expression. 

1. One
2. Zero
3. None. 

Since asymptotes exist for rational (p/q form) expressions only, this means there is always a numerator and denominator. You can figure it out by comparing both terms.

Case - 1: 

If the upper value and lower value of an expression are the same (in terms of degree or power), the leading coefficients are simplified to get the asymptote value. For example; you have an expression (2x² - 3) / ( 7x²).

The leading coefficients are the ones with the highest degree of exponents. In our example, these values are 2x² and 7x². So by dividing these we get 2/7. And this is the horizontal asymptotic value.  

Case - 2:

In a scenario where the denominator is greater than the numerator (proper fraction), the horizontal asymptote occurs at 0. This means f(x) gets closer to zero with the increase in the value of x.

For example, the horizontal asymptotes in x / x² + 1 exist on the zero.

Case - 3:

When none of the above conditions are present, the horizontal asymptote simply does not occur. 

Slant Asymptote:

There are again two cases; it exists or it does not exist. It is also found by comparing numerator and denominator.

Case - 1:

When the expression is improper and the numerator is one degree greater than the denominator, the slant asymptotes occur. 

To find its value, you will have to perform polynomial long division. Ignore the remainder at the end. For instance, if we find the asymptotic value for (x² + 3x + 2) / (x - 2) then we get (x + 5) with a remainder 12. 

So the linear equation to which the curve nears is y = x + 5.

Case - 2:

In the case in which the numerator is greater than the denominator with more than one degree, no horizontal or oblique asymptote is possible. 

Vertical Asymptote:

Vertical asymptotes are drawn where the value of the bottom function is zero, at the roots. It can exist alongside horizontal and slant asymptotes. But it is important that the expression is in its most simplified form.

Since there can be one, two, or many roots of a polynomial expression, more than one vertical asymptote is possible for one function. They can be multiple in number. 

Fun fact: y = Tan(x) has infinite asymptotes.

For example: f(x) = (2x - 7) / (x² - 5x - 36)

To find the vertical asymptotic value, take the bottom value and factorize it. 

x² - 9x + 4x - 36 = 0

x(x - 9) + 4 (x - 9) = 0

(x + 4)(x - 9) = 0 

The roots are x = -4 and x = 9. These are the two points where vertical asymptotes occur.