Binomial Theorem Calculator

The binomial expansion calculator is an important tool in algebra and calculus. It expands a polynomial expression and finds its sum. 

You can see all of the steps below the answer which will explain how to solve the expression yourself. The calculator accepts larger values, even the ones with more than 10 digits. 

What is binomial theorem?

It is a theorem or formula that solves polynomial equations with two terms. Bi means two hence a polynomial with two terms is called binomial.

Some examples of binomial expressions are:

• 2x - 9y
• x² - z
• 84x - y² e.t.c. 

You can notice that in each example, both of the two terms are separated by plus or minus operation. 

The binomial theorem is used to expand or find the solution of such expressions that have some exponents because they get a little tricky and lengthy to solve by hand. E.g (x² - y)⁸

Binomial theorem derivation:

To learn what a binomial theorem is, we start with the basics. The simplest binomial expression is (x + y). Its power or exponent here is 1. 

Note: A power 0 e.g 7⁰ means 7 should be written 0 times. Which eventually means 7⁰ = 1. 

Now, if we gradually increase the power of (x + y) and solve, we might get somewhere.

(x + y)⁰ = 1 

(x + y)¹ = x + y

(x + y)² = (x + y) * (x + y) = x(x + y) + y(x + y) = x² + 2xy + y²

Similarly,

(x + y)³ = x³ + 3x²y¹ + 3x¹y² + y³

(x + y)⁴ = x⁴ + 4x³y¹ + 6x²y² + 4x¹y³ + y⁴

Things get complicated from here on. Because you can’t possibly imagine expanding (x + y)¹¹. This is where we make use of the binomial series theorem. 

If you look at the formulas we got after multiplication, you will be able to see a pattern. 

Exponents:

Take (x + y)³. Each term in the formula has some power. Notice that the value of exponents decreases for the first variable and increases for the second variable along with the expansion from left to right. 

For the first variable x, the powers go like 3,2,1,0, and for the second variable, the power has the ascending order i.e 0,1,2,3. 

See the order of operation calculator for ascending and descending orders. We can write it algebraically as:

x^n-k y^k

Variables are sorted, now let’s move to their coefficients.

Coefficients:

The pattern of coefficient makes more sense if you are familiar with Pascal’s triangle. For (x + y)⁴, this triangle is :

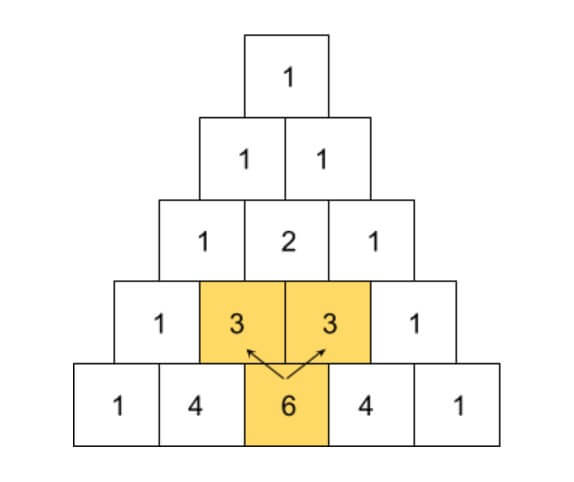
The boxes at the edge remain the same i.e 1. And every other box is the addition of the two boxes overlapping above it. For example, 6 has two 3 and 3 boxes above it: 3+3=6. 

To write it in the formula form, we use the combination. It is written as: 

ⁿC_k = n! / k!(n-k)!

Where n is the exponent value and k is the starting term that is 0 in the binomial theorem. The "!" symbol is factorial. ⁿC_k is also written as (ⁿ_k).

Let’s see if this formula holds true for (x+y)⁴:

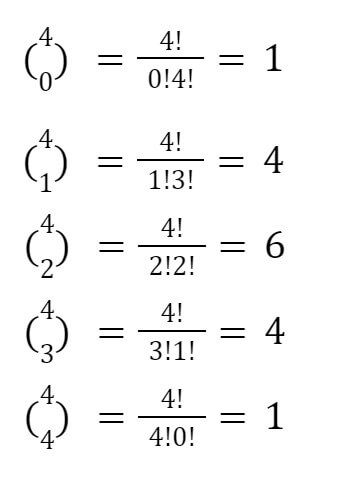
So now, we have formulas for both variables and coefficients. But to write them together so that the final thing makes sense, we use the summation symbol.

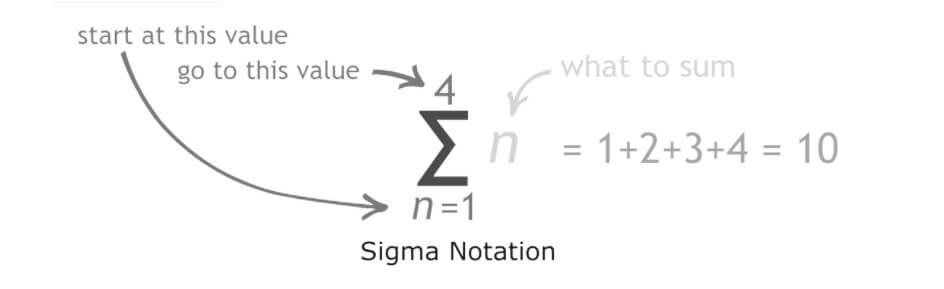
So the binomial theorem is:

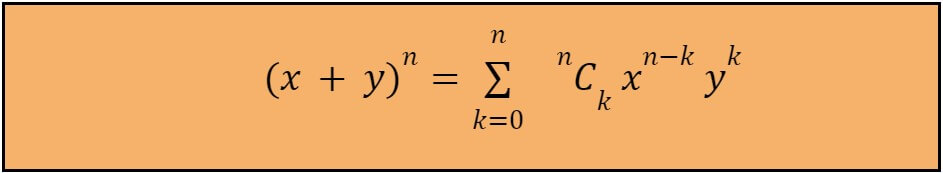
Mostly, you will find this theorem written with variables a and b in place of x and y.  

A point to note: There are always n+1 terms in the expanded binomial expression. 

As a final step, we will take real numbers along the variables to actually solve it. 

Example:

Solve (2a + 5)⁴.

Solution:

Step 1: Identify the values.

x = 2a

y = 5

n = 4

Step 2: Put the values in the formula and solve the coefficients.

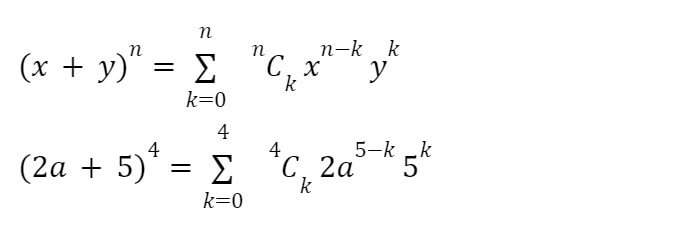
The coefficient values for (x + y)⁴, as we have discussed many times before, are 1,4,6,4,1. We will skip this part of the step.

Step 3: Now, calculate the answer to every value of k from 0 to 4.

Step 4: Write in the form of a series. 

(2a + 5)⁴ = 16a⁴ + 160a³ + 600a² + 1000a + 625