To calculate result you have to disable your ad blocker first.
Boolean Algebra Calculator
Enter the boolean expression in the boolean algebra calculator to find the truth table and the nature of the expression.
Table of Contents:
The boolean algebra simplifier is a physics and algebra-related tool. It finds the truth table of the inserted boolean expressions. You can enter all of the boolean operators in the boolean algebra simplifier.
Below is a brief introduction to Boolean algebra and its functions. Learn to make truth tables by scrolling down. You might also like the binary calculator.
What is boolean algebra?
The binary algebra simplifies the logical expressions and uses the binary values 1 and 0. In boolean algebra, 1 means truth and 0 mean false.
It is used mainly in computer programming. But apart from that, it is also used in set theory, circuit physics, and Statistics. Boolean algebra is used in mechanics for machines that exist in two states.
Remember that boolean and binomial are two different concepts. People tend to get confused between them as both deal with two terms.
Boolean operators
Elementary algebra uses basic math functions such as division and addition. Whereas binary algebra has different operations.
The three main boolean operators are listed below along with their notation, operator, and Venn diagram.
Conjunction/And operation:
The And function means both terms (A And B) should be true for an argument to be true. 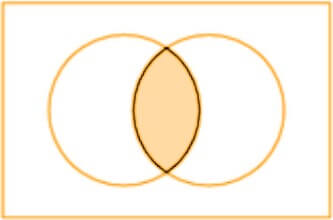
If even one is false or both are false, the argument will be false. It is represented by () notation. Using the (*) sign is also acceptable.
It imitates the multiplication operation. The truth table for AND function is:
A | B | A∧B | A∧B |
0 | 0 | 0*0 | 0 |
0 | 1 | 0*1 | 0 |
1 | 0 | 1*0 | 0 |
1 | 1 | 1*1 | 1 |
Disjunction/OR operations:
When this operator is applied, if even one of the terms is true (A Or B), the argument will be true. This is similar to the addition operation. 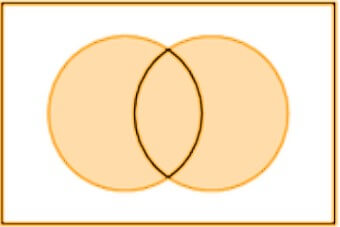
The notation of OR function is (). The addition symbol (+) is also one way of writing it.
Its truth table is given below:
A | B | A∨B | A∨B |
0 | 0 | 0+0 | 0 |
0 | 1 | 0+1 | 1 |
1 | 0 | 1+0 | 1 |
1 | 1 | 1+1 | 1 |
Negation/Not operation:
The Not operation means the inverse of the given value. Its notation is (). It works like the complement(') or Minus (-)operation. 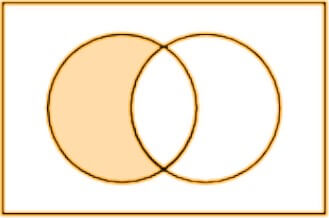
This Venn diagram is of expression A+ (-B).
One’s complement calculator works in the same way.
So you can also write A’ or -A. The truth table for the Not operation is:
A | A’/-A |
1 | 0 |
0 | 1 |
How to find the truth table for boolean expressions?
If the expression is complex, it is suggested to break it down into smaller expressions and write the truth tables one by one.
You can use the boolean algebra simplifier with steps to find the truth tables. See the example below if you want to learn more.
Example:
Find the truth table for -(P*(-P+Q))+Q
Solution:
Step 1: Break the expression.
First : (-p+q) = A
Second : (p*A) = B
Third: (-B+q)
Step 2: Make the first table.
- Apply the Not operation on P.
- Then apply the OR operation on p and q.
p | q | -p | -p + q = A |
0 | 0 | 1 | 1 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 |
1 | 1 | 0 | 1 |
Step 3: Make the second table.
Apply the And operation.
p | A | p*A = B |
0 | 1 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Step 4: Make the third table.
- First, use the Not operation on B.
- Then use the OR operation.
B | -B | q | -B + q |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 |
0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 |
It is the final answer. You can write all of the three tables as one.
Example 2:
Make the truth table for:
(A*-B)+(-A*B)
Solution:
A | B | -B | A*-B | -A | -A*B | (A*-B)+(-A*B) |
0 | 0 | 1 | 0 | 1 | 0 | 0 |
0 | 1 | 0 | 0 | 1 | 1 | 1 |
1 | 0 | 1 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 0 | 0 | 0 | 0 |
Truth table for all boolean/binary operations:
There are some more operations used in boolean algebra for example NAND, NOR, XOR e.t.c. See the table below if you want to know more about these operations.
Under the first four rows of the truth table, there is a property/law check.
p | q | F | NOR | ↚ | ¬p | ↛ | ¬q | XOR | NAND | AND | XNOR | q | → | p | ← | OR | T |
T | T | F | F | F | F | F | F | F | F | T | T | T | T | T | T | T | T |
T | F | F | F | F | F | T | T | T | T | F | F | F | F | T | T | T | T |
F | T | F | F | T | T | F | F | T | T | F | F | T | T | F | F | T | T |
F | F | F | T | F | T | F | T | F | T | F | T | F | T | F | T | F | T |
Com | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
Assoc | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
Adj | F | NOR | ↛ | ¬q | ↚ | ¬p | XOR | NAND | AND | XNOR | p | ← | q | → | OR | T | |
Neg | T | OR | ← | p | → | q | XNOR | AND | NAND | XOR | ¬q | ↛ | ¬p | ↚ | NOR | F | |
Dual | T | NAND | → | ¬p | ← | ¬q | XNOR | NOR | OR | XOR | q | ↚ | p | ↛ | AND | F | |
L id | F | F | T | T | T,F | T | F | ||||||||||
R id | F | F | T | T | T,F | T | F | ||||||||||
References
- What is Boolean algebra? Study.com | Take Online Courses. Earn College Credit. Research Schools, Degrees & Careers. (n.d.)
- Boolean algebra calculator by Allmath
- Boolean algebra truth tables. Basic Electronics Tutorials.
