To calculate result you have to disable your ad blocker first.
ADVERTISEMENT
Confidence Interval Calculator
To find the confidence interval, select type, enter the values in the required input boxes, and hit the calculate button using confidence interval calculator
Table of Contents:
The confidence interval calculator uses the standard deviation, mean, and sample size to find an interval for the estimation of the true population mean. Users can enter raw data as well as summary data.
Find 80, 90, 95, and even 99.9 percent confidence levels through this confidence interval calculator. For raw data, the calculator finds the necessary values separately and automatically inputs them in the required place.
How to use this confidence interval calculator?
To use the confidence interval calculator, you will need to choose the type of calculator. For already calculated values;
- Select “Mean and SD” type.
- Pick a confidence level.
- Enter mean, standard deviation, and sample size.
- Click calculate.
For raw data
- Choose the “raw data” option.
- Enter the values. It is better if n > 30.
- Click calculate.
The required values will be calculated to find the confidence interval. Again choose the “mean and SD” type. The values calculated previously will have been automatically inputted. Simply click calculate.
What is a confidence interval?
An interval represents the range. In statistics, a confidence interval is a range of numbers in which the actual population means lies. It is related to a certain percent of confidence level.
It is never 100 percent. If it were then there will be no need for the confidence interval, you could simply know the population means.
Confidence interval example:
Say you went to a thrift bookstore. You read the prices of 20 books on a shelf and the mean was 7. The standard deviation of the prices of books is 2.
The 99.9 percent confidence interval (the calculations will be taught later in the article) is:
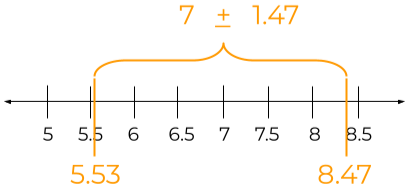
Where 1.47 is the margin of error. This interval tells that there is a 99.9 percent chance that if the actual price of each book on the rack is taken into account, the mean will be somewhere between 5.53 and 8.47.
But there is also a 0.01 percent chance that the mean will be outside of this interval. Or to put in other words, if you count the mean 1000 times, it is possible one time it will not fall in this interval.
To know which time the calculation of the mean of prices was correct, 999 times when the answer was in the interval or the 1 time when it was not, is impossible unless the confidence level is 100.
100 percent confidence tells no matter how many times you find the mean, be that 1000 or million times, it should be the same. Then it becomes a population parameter.
Confidence interval formula:
The formula used to find the confidence interval using the mean, standard deviation, and the sample size is:
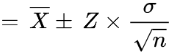
Here,
- The X bar represents the mean of the sample values.
- Z is the z-score.
- And sigma (standard deviation) over under-root n (sample size) represents the standard error.
How to find the confidence interval?
If the values required in the confidence interval formula are already given or calculated, then just put them in the formula.
But if the data provided is raw, you will need to do some calculations. The process is very long so we suggest the calculator above.
Sample count:
Count the number of values present in the sample.
It is suggested that the sample data should be equal to or greater than 30 values. This way the population standard deviation (sigma ????) and sample standard deviation (s) will be the same.
Mean of the sample:
Find the mean of the sample by adding all of the sample values and dividing this sum by the total count. The formula is
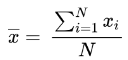
Standard deviation:
For the next step, find the standard deviation using the formula below:
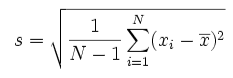
As said before sample standard deviation is the same as the population standard deviation(sigma ????) for x>30 which we need in the confidence interval formula.
The value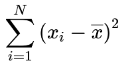 
is called the sum of squares.
Standard deviation is strongly related to variance. See the variance calculator.
Standard error:
The standard error can be calculated by dividing the population standard deviation by the under-root of the sample count.
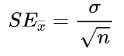
Z-score:
To find the z-score, there is an already calculated z-score table. It contains all of the confidence levels. Choose the one you want.
| Confidence Interval | Z |
| 80% | 1.282 |
| 85% | 1.440 |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
| 99.5% | 2.807 |
| 99.9% | 3.291 |
Now multiply this z score by the standard error. This value is called the margin of error. It tells how much to the right or left of the calculated sample mean, the population means may fall.
Find the range using these formulas:
Upper bound = mean + margin of error.
lower bound = mean - margin of error
Example:
Find the 95 percent confidence interval of the following data.
12, 32, 34, 11, 6, 9, 14, 50, 41, 10, 10, 1, 0, 11, 23, 44, 19, 21, 31, 0, 22, 33, 44, 4, 3 , 37, 40, 35, 17, 2, 33, 44.
Solution:
Step 1: Count the values and find the mean.
N = 32
Mean (x̄) = (12 + 32 + 34 + 11 + 6 + 9 + 14 + 50 + 41 + 10 + 10 + 1 + 0 + 11 + 23 + 44 + 19 + 21 + 31 + 0 + 22 + 33 + 44 + 4 + 3 + 37 + 40 + 35 + 17 + 2 + 33 + 44) / 32
Mean (x̄) = 693 / 32
Mean (x̄) = 21.66
Step 2: Calculate standard deviation.
Finding the sum of the squares.
= (12 - 21.66)2 + (32 - 21.66)2 + (34 - 21.66)2 + (11 - 21.66)2 + (6 - 21.66)2 + (9 - 21.66)2 + (14 - 21.66)2 + (50 - 21.66)2 + (41 - 21.66)2 + (10 - 21.66)2 + (10 - 21.66)2 + (1 - 21.66)2 + (0 - 21.66)2 + (11 - 21.66)2 + (23 - 21.66)2 + (44 - 21.66)2 + (19 - 21.66)2 + (21 - 21.66)2 + (31 - 21.66)2 + (0 - 21.66)2 + (22 - 21.66)2 + (33 - 21.66)2 + (44 - 21.66)2 + (4 - 21.66)2 + (3 - 21.66)2 + (37 - 21.66)2 + (40 - 21.66)2 + (35 - 21.66)2 + (17 - 21.66)2 + (2 - 21.66)2 + (33 - 21.66)2 + (44 - 21.66)2
= 7528
(Standard deviation)2 = 1/(32-1) * 7528
(Standard deviation)2 = 7528 / 31
(Standard deviation)2 = 242.8
Taking square root on both sides.
Standard deviation = 15.5
Step 3: Find the standard error.
Since the n>30, ???? = s.
Standard error = 15.5 /√32
= 2.74
Step 4: See the z score for 95 percent confidence level and put the values in the confidence interval formula.
Z score for 95 percent is 1.960. Putting in the formula.
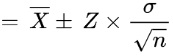
= 22.7 ± (1.960)(2.74)
= 22.7 ± 5.3704
The range or interval is [16.3,27].
ADVERTISEMENT