Harmonic Mean Calculator

The harmonic mean calculator is a statistical tool to find the harmonic mean of values or data. 

The calculator finds the mean along with the steps. It also displays the formula of the harmonic mean. The calculations are done very fast.

Scroll down to know more about the harmonic mean, its formula, and how to calculate?

How to use Harmonic Mean calculator?

To use this tool, you will have to enter the numbers separated by commas. After that press enter or click “calculate”.

What is Harmonic mean?

The harmonic mean can be defined as:

“A fraction written in decimal form, whose numerator is the total number of entries and denominator is the sum of reciprocals of each entry.”

Harmonic mean is one of the Pythagorean means, the three important central tendencies. It has its uses in physics, geometry, stats, and finance. 

Harmonic mean formula:

The formula used for the calculation of harmonic mean is given below.

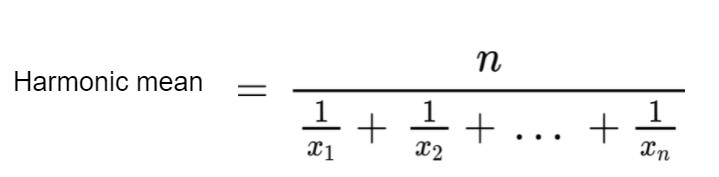
In this equation:

• n is the number of entries.
• x₁ is the first entry.
• x_n is the last entry.

The harmonic mean formula of 2 and 3 values is further simplified to make the process easy. 

For 2 values, H.M = 2 * x * y / (x + y)

For 3 values, H.M = 3 * x * y * z / (x + y +z)

Calculating H.M using G.M and A.M

If you have the arithmetic mean and geometric mean of n values, then you can easily calculate the harmonic mean by this formula: 

H.M = G.M2 / A.M

The harmonic mean is smaller than both the geometric mean and arithmetic mean i.e H.M < G.M < A.M.

How to calculate the harmonic mean?

To find the harmonic mean:

1. Count the values.
2. Find the reciprocal of each number or reading.
3. Add all of the reciprocals.
4. Divide the total number of values (n) by the sum of the reciprocals. 

Example 1:

For the given set of data, find the harmonic mean.

(1, 17, 7, 41, 2)

Solution:
Step 1: Count the number of values.

There are 5 values.

Step 2: Find the reciprocal of each value.

1/1 = 1

1/17 = 0.0058

1/7 = 0.1429

1/41 = 0.0244

1/2 = 0.5

Step 3: Add all reciprocals.

= 1 + 0.0058 + 0.4129 + 0.0244 + 0.5

= 1.7261

Step 4: Divide the total number of values by this sum.

= 5 / 1.7261

= 2.89675

Example 2:

If the G.M of a set of data is 2√3 and A.M is 6. Then find its harmonic mean.

Solution:

Step 1: Identify the given data.

A.M = 6

G.M = 2√3

Step 2: Use this data in the formula.

H.M = G.M² / A.M

H.M = (2√3)² / 6

H.M = (4*3) / 6

H.M = 12 / 6

H.M = 2