Washer Method Calculator

Washer Method Calculator

Washer Method Calculator is used to determine the volume of the solid revolution of the hole along the x-axis using a definite integral.

What is washer method?

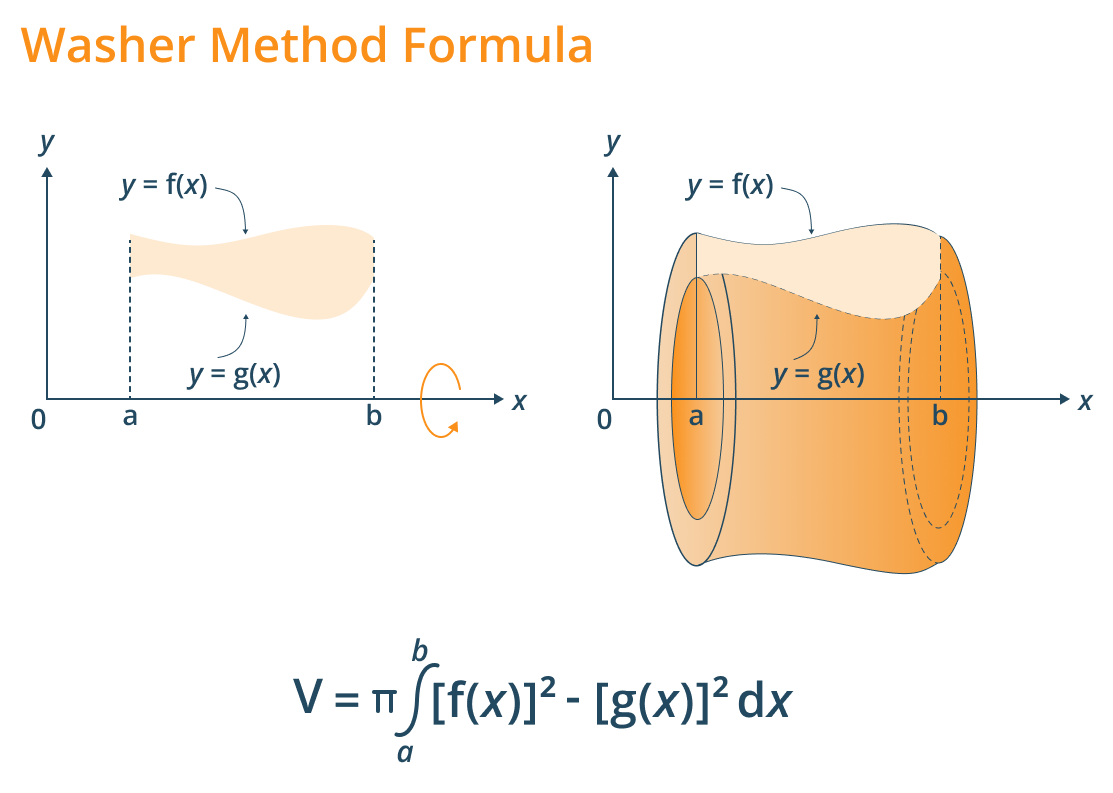
Washer method is used to find the volume of the three-dimensional solid objects across the cross-sectional like the washer and ring. It is the modified method to determine the volume of a solid disc with holes. 

How does the washer method work?

In this method determine the volume of the washer with the help of two functions that rotate around the x-axis. To determine the volume create the slices of the shape according to the function and determine the values of the functions.

Then apply definite integral with the square of the first function is subtracted by the definite integral value of the square of the second function. At the end, all values multiply with the constant “Pi”.

Formula of the washer method

The washer method formula is defined as the difference of the squares of the two functions under the definite integral with its upper and lower bounds. The graphical representation of the washer and its formula is presented below.

V = π ∫_a^b [f(x)² - g(x)²] dx

Where,

• “a” = lower limit of the integral
• “b" = upper limit of the integral
• “π” = mathematical constant “Pi” ≈ 3.14159

How to evaluate the volume with washer method?

Our above washer method calculator is an easy to use tool that helps to determine the volume of the solid objects. However, if you want to calculate it manually then follow the below examples.

Example 1

Find the volume of the solid revolution which is bound by the upper curve “f(x) = 2x²” and the bottom curve is “g(x) = 7y²” in the interval [2, 4].

Solution

Step 1: write the given functions and interval values.

f(x) = 2x²,                                                   g(x) = 7y²

Upper limit = 4,                                         lower limit = 2

Step 2: Put the values in the washer formula.

V = π ∫_a^b [f(x)² - g(x)²] dx

= π ∫₂⁴ [(2x²)² – (7y²)²] dx

Step 3: Solve the squares of the function.

= π ∫₂⁴ [4x⁴ – 49y⁴] dx

Sep 4: Apply the difference rule of integral and simplify the integral with respect to “x”.

= π {∫₂⁴ (4x⁴) dx – ∫₂⁴ (49y⁴) dx}

= π {4 ∫₂⁴ (x⁴) dx – 49 ∫₂⁴ (y⁴) dx}

Apply the power formula of the integral in the first term.

= π {4 (x⁴⁺¹/4+1) |₂⁴ – 49 (y⁴x) |₂⁴}

= π {4 (x⁵/5) |₂⁴ – 49 (y⁴x) |₂⁴}

= π {4/5 (x⁵) |₂⁴ – 49 (y⁴x) |₂⁴}

Step 5: Apply the upper and lower limits of the integral by using the fundamental theorem of calculus and simplify the terms.

= π {4/5 ((4)⁵- (2)⁵) – 49 [y⁴ (4-2)] }

= π {4/5 (1024 - 32) – 49 [y⁴ (4-2)] }

= π {4/5 (992) – 49 [y⁴ (2)] }

Using distribution law multiply the “pi” with both terms and also simplify the fraction.

= π 793.6 – π 98 y⁴

Step 6: Put the values of the “pi” and simplify the terms.

V = 3.14 × 793.6 – 98 × 3.14 y⁴

V = 2491.9 – 307.72 y4

Example 2

Find the volume of the solid revolution which is bound by the upper curve “f(x) = x + 3” and the bottom curve is “g(x) = y + 2” in the interval [2, 3].

Solution

Step 1: write the given functions and interval values.

f(x) = x + 3,                                                g(x) = y + 2

Upper limit = 3,                                         lower limit = 2

Step 2: Put the values in the washer formula.

V = π ∫_a^b [f(x)² - g(x)²] dx

= π ∫₂³ [(x + 3)² – (y + 2)²] dx

Step 3: Solve the sum of squares of the function by the square formula such as “(a+b)² = a² + 2ab + b²”.

= π ∫₂³ [(x + 3)² – (y + 2)²] dx

= π ∫₂³ [(x² + 6x + 9) – (y² + 4y + 4)] dx

= π ∫₂³ [x² + 6x + 9 – y² – 4y – 4] dx

= π ∫₂³ [x² + 6x – y² – 4y + 5] dx

Sep 4: Apply the difference rule of integral and simplify the integral with respect to “x”.

= π {∫₂³ (x²) dx + ∫₂³ (6x) dx – ∫₂³ (y²) dx - ∫₂³ (4y) dx + ∫₂³ (5) dx}

= π {∫₂³ (x²) dx + 6 ∫₂³ (x) dx – ∫₂³ (y²) dx – 4 ∫₂³ (y) dx + ∫₂³ (5) dx}

Apply the power rule and constant rule of the integral.

= π {(x²⁺¹/2+1)|₂³ + 6 (x¹⁺¹/1+1)|₂³  –  (x y²)|₂³– 4(x y)|₂³ + 5(x)|₂³}

= π {(x³/3)|₂³ + 6 (x²/2)|₂³  –  (x y²)|₂³ – 4(x y)|₂³ + 5(x)|₂³}

= π {1/3(x³)|₂³ + 3 (x²)|₂³  – (x y²)|₂³ – 4(x y)|₂³ + 5(x)|₂³}

Step 5: Apply the upper and lower limits of the integral by using the fundamental theorem of calculus and simplify the terms.

= π {1/3 [(3)³ – (2)³] + 3 [(3)² – (2)²] – y² [(3) – (2)] – 4y [(3) – (2)] + 5 [3-2]}

= π {1/3 [27 – 8] + 3 [9 – 4] – y² [3 – 2] – 4y [3 – 2] + 5 [3-2]}

= π {1/3 [19] + 3 [5] – y² – 4y + 5}

= π {19/3 + 15 – y² – 4y + 5}

= π {6.33 + 15 + 5 – y² – 4y}

= π {26.33 – y² – 4y}

Using distribution law multiply the “pi” with both terms and also simplify the fraction.

= π 26.33 – π y² – 4 π y

Step 6: Put the values of the “pi” and simplify the terms.

V = (3.14 × 26.33) – (3.14 × y²) – (4 × 3.14 × y²)

V = 82.67 – 3.14 y2 - 12.56 y2