To calculate result you have to disable your ad blocker first.
Integral Calculator with Steps
Enter the function, variable, upper and lower bound limit. Select the definite or indefinite option. Hit the Submit button to evaluate the integral step by step using integral calculator.
Table of Contents:
Integral Calculator
Integral calculator is an online tool that calculates the antiderivative of a function. It works as a definite integral calculator as well as an indefinite integral calculator and lets you solve the integral value in no time.
Integral solver shows you all of the steps required to evaluate the integrals. It performs the integration of a function by parts and solves the integrals with two different methods.
What is an integral?
An integral is the reverse of the derivative. It can be used to determine the area under the curve.
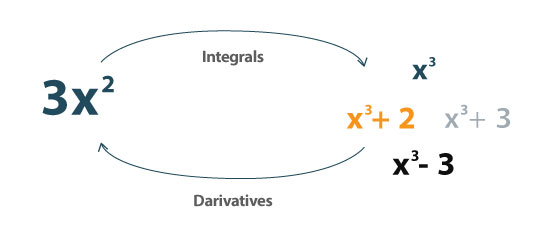
It can be defined as:
“An integral assigns numbers to functions in a way that can describe displacement, area, volume, and other concepts that arise by combining infinitesimal data. Integration is one of the two main operations of calculus; its inverse operation is differentiation (taking derivatives).”
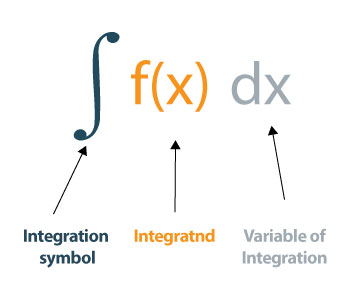
How to evaluate the integral?
You may want to know how to solve integrals manually. It can be somehow annoying for the ones who are just starting with integrals. But, don’t worry. We will demonstrate the calculations with examples so that you can grasp it easily.
Let’s use an example to understand the method to calculate the definite integral.
Example – Definite integral
For the function f (x) = x – 1, find the definite integral if the interval is [1, 10].
Solution:
Step 1: Determine and write down the function F(x).
F (x) = x – 1
Interval = [1, 10]
Step 2: Evaluate the integral of the function and add the constant.
= ∫ (x−1) dx = (x2/2) – x + C
Step 3: Calculate the values of upper limit F(a) and lower limit F(b).
As, a = 1, and b = 10,
F(a) = F(1) = (12/2) - 1 = -0.5
F(b) = F(10) = (102/2) - 10 = 40
Step 4: Calculate the difference of upper limit F(a) and lower limit F(b).
F (b) – F (a) = 40 – (-0.5) = 40.5
You can use an integral calculator above if you don’t want to indulge in integral calculations.
Example – Integral of a trigonometric function
For the function f(x) = sin(x), find the definite integral if the interval is [0, 2π].
Solution:
Step 1: Write down the function.
F (x) = sin (x)
Interval = [0, 2π]
Step 2: Evaluate the integral of the function and add constant C.
= ∫ sin(x)dx = - cos(x) + C
Step 3: Calculate the values of upper limit F(a) and lower limit F(b).
As, a = 0, and b = 2π,
F(a) = F(0) = -cos(0) = -1
F(b) = F(2π) = -cos(2π) = -1
Step 4: Calculate the difference of upper limit F(a) and lower limit F(b).
F (b) – F (a) = -1 - (-1) = -1 + 1 = 0
Use integral solver above to solve a trigonometric integral in a fraction of seconds.
Examples of integral
Here are some more examples of intergal solved by our integral finder.
| Functions | Integration |
| integral of 1/x | log x + C |
| integral of 2^x | 2x/ln2 + c |
| integral of 2x | x2 + C |
| integral of x | x2/2 + C |
| integral of e^x | e^x + C |
| integral of 1/e^x | -e-x + C |
| integral of 1 | x + C |
| integral of x^x | Non integrable function |
| integral of a^x | ax/ln(a) + C |
| integral of 1/x^2 | -1/x + C |
| integral of ln(x) | xlnx - x + C |
| integral of sec^2x | tan(x) + C |
References:
- What is integral? with Example, from socratic.org
- Definition of INTEGRAL. by merriam-webster.