Fraction Simplifier

The fraction reducer helps users to solve a fraction to its simplest form. This tool can simplify both types of fractions i.e proper and improper.

The calculator gives the labeled and detailed process of reducing fractions and you can reset it as many times as you want. 

How to use this tool?

Follow the given instruction to use the fraction-simplifier.

1. Enter the fraction carefully.
2. Hit “Calculate”.
3. Click on “Show steps” for the full process.

You can also try using this tool on mixed fractions by converting them to improper fractions. For such conversions, a mixed to improper fractions calculator can come in handy.

Fraction and its types

The numbers in p/q form are called fractions. It has three main types: proper, improper, and mixed.

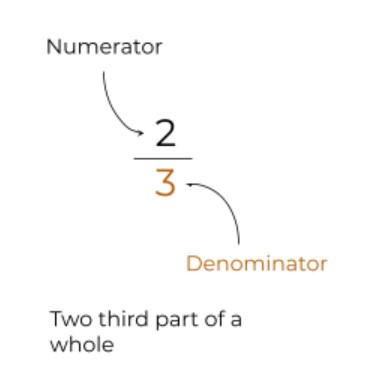
An improper fraction has a numerator higher than its denominator. A proper fraction is the opposite of a proper fraction with a denominator higher than its numerator. 

How to reduce a fraction?

A fraction is simplified by dividing both values using the same number. Note that the values should be completely divisible by the chosen number without any remainder.

A fraction can be simplified using different techniques. Keep reading to learn these methods. These are:

• GCF 
• Division ladder 
• Trial and error method

The fraction reducer uses the GCF technique. Before diving into the details of all these techniques, try our decimal number calculator. Decimals are also fractions but they are not written in p/q form. 

Using GCF:

The GCF is the highest number that can divide both the denominator and the numerator completely. Below is an example of using this method.

Example:

Solve the fraction 12/18 using the GCF.

Solution:

Step 1: Find the GCF of 12 and 18.

The GCF of 12 and 18 is 6.

Step 2: Divide both numbers by 6.

12 / 6 = 2

18 / 6 = 3

Step 3: Write in the fraction form.

= 2/3

The division ladder method:

The division ladder technique is used in other fields as well, for instance in LCM. 

In this method, you start diving both numbers by the smallest common multiple. The number must be a multiple of both numbers. See the solved example:

Reduce the fraction 25/50 using the division ladder method.

Solution:

Start Dividing by the lowest natural number after 1.

2 is not a multiple of 20 and 50. Neither are 3 and 4. But 5 can divide both numbers. So, using 5 in the ladder method.

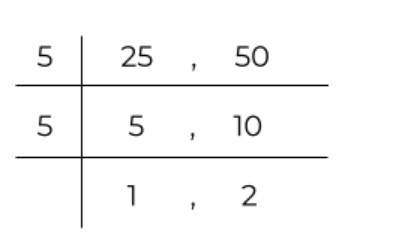
Now, the 1 and 2 at the end cannot be further simplified using the same number. Moreover, they are prime numbers. Therefore we write 1 and 2 in the fraction form:

= 1/2

Trial and error method:

This technique is purely based on guesses and assumptions. You can think of it as another way of using the division ladder technique. Just in this method, you don’t make the ladder.

Example: 

What is the simplest form of 15/27?

Solution:

Let’s start making gusses. 

Guess 1: 2 can divide both numbers completely.

Test: 15/2 = 7.5 , 27/2 = 13.5. This means 2 is not a valid multiple.

Guess 2: 3 can divide both numbers completely.

Test: 15/3 = 3 , 27/ = 9. The guess was correct.

The fraction is 3/9. Since 9 is not a prime number, we have to consider the possibility of simplifying it more.

Guess 1: 2 can divide.

Test: 3/2 = 1.5 , 9/2 = 4.5

Guess 1: 3 can divide.

Test: 3/3 = 1 , 9/3 = 3. Hence, 3 is again the required multiple.

The simplest form of 15/27 is 1/3. 

Most people do all this guessing in their heads.