Median Calculator

Median Calculator

Median calculator is used to find the median of the large data set and provides information on the mean, mode, and range of the data set.

What is the median?

Median is the middle/central point of the data set that can distribute the values into two halves such as the small values of the data set and large values of the data set or the middle point relies in between these numbers.

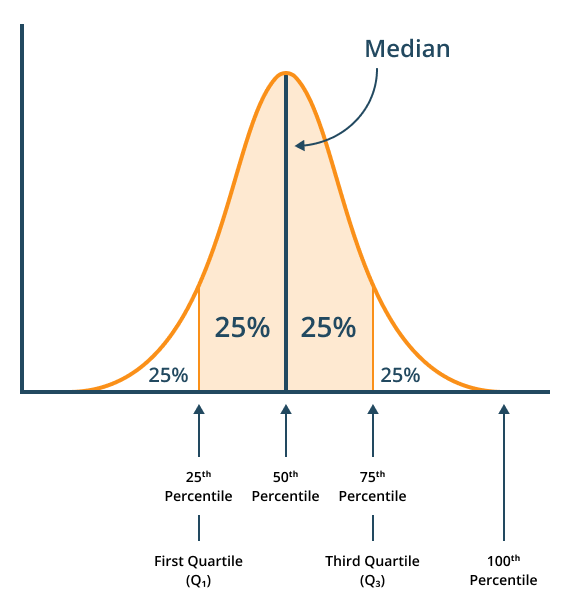
The median is also known as the midpoint of the data set if we have a hundred terms in a data set then the 50^th-number is the median of this number.

Due to this 50^th-percentile of the data set also represents the median of a data set which is denoted as “P₅₀” while in terms of the quartile is known as the second quartile of the data set denoted by the “Q₂”.

Median Formulas

There are two basic formulas of median depending on the total number of data sets such as even or odd. If the number of the data set is even then the median is an average/arithmetic mean of the two middle terms.

While on the other hand if the number of values is odd then the middle term of the data set is the median of the data set. The formulas of the median for even and odd numbers of data sets can be stated as,

If “n” is odd then its formula can be stated as,

x = ((n+1) /2)th term  

If “n” is even then its formula can be stated as,

x = [(n/2)th term + ((n/2) + 1)th term]/2

Where,

• n = total number of the data set
• x = shows the chosen term from the data set in ascending order

Steps to calculate the median

To determine the median of the data set follow the below steps.

• Firstly, arrange the data values (from least to greatest number) in ascending order.
• Count the total number of the data set if even or odd.
• Lastly, for the selection of terms use the appropriate formula according to the number of data sets.

Example 1:

Find the median of the given data set such as, {1, 3, 5, 7, 9, 4, 6}.

Solution:

Step 1: Arrange the data values in ascending order and note the total number of the data set.

Data set = {1, 3, 4, 5, 6, 7, 9} ------------>(i)

n = 7

Where “n=7” that is an odd number.

Step 2: Use the odd number formula of median and find the term.

x = ((n+1) /2)th term  

= ((7+1) /2)^th term  

= (8/2)^th term  

x = 4^th term  

Hence, see the 4^th-term in the data set of eq (i).

Thus, Median = 5

Example 2:

Evaluate the median of the given data set such as, {13, 23, 12, 44, 23, 55}.

Solution:

Step 1: Arrange the data values in ascending order and note the total number of the data set.

Data set = {12, 13, 23, 23, 44, 55} ------------>(i)

n = 6

Where “n=6” that is an even number.

Step 2: Use the even number formula of median and find the term.

x = [(n/2)th term + ((n/2) + 1)th term]/2

= [(6/2)^th term + ((6/2) + 1)^th term]/2

= [3^th term + (4)^th term]/2

Step 3: Place the value of the 3^th-term and 4^th-term from the eq (i).

= 23 + 23/2

= 23

Thus, Median = 23