Fraction to Decimal Calculator

Fraction to decimal calculator is used by thousands of users to convert fractions into decimals, daily. The fraction to decimal converter will first simplify the fraction, either proper or improper, and then provide its decimal form. 

How to use this calculator?

Simply yet carefully enter the fraction and press enter. That’s all you have to do.

Fractions to decimals

As you may already know, fractions are exact alternates of decimals.

A fraction ¼ is also written as 0.25 in decimal form. Both of these values can be replaced in a calculation with each other and the result will remain the same. 

But both of these are preferred over each other according to the type of computation you are performing. Below you will learn all the processes that can be used to convert the fraction to decimals. 

Try the opposite tool, decimal to fraction converter. 

How to convert fractions to decimals?

There are 3 different techniques for converting fractions to decimals. 

1. Long Division method.
2. Simplifying by GCF.
3. Making Denominator a power of 10.

Let’s learn the details of all manual methods and see their solved examples.

Long division method:

The most common method for this purpose. In long division, you simply write the numerator of the fraction as dividend and the denominator as a divisor. After that division is performed. 

Example: 

Solve the fraction 26/8 to find its decimal form.

Solution:

Step 1: Identify the values.

Dividend = 26 

Divisor = 8 

Step 2: Write in the long division symbol and solve.

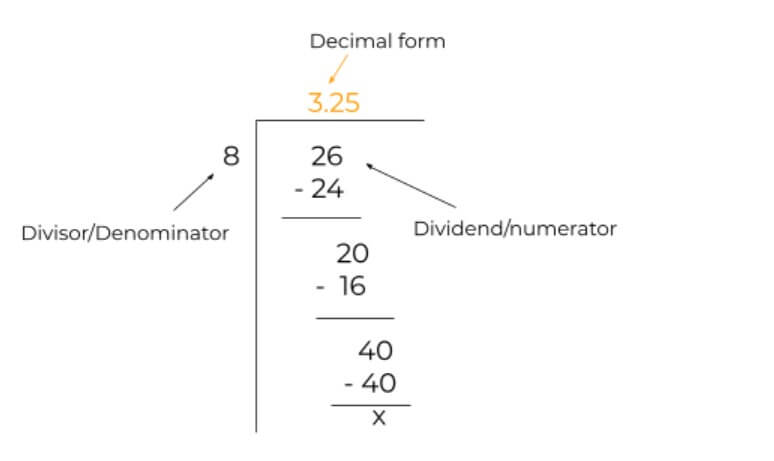
The decimal form of 26/8 is 3.25.

Simplifying by GCF:

This method also involves division but before that fraction is reduced to its simplest form. The fraction to decimal calculator uses the same method. 

To reduce a fraction, you have to find its GCF and after dividing upper and lower values by GCF, the reduced fraction can be easily converted into decimals, even in mind sometimes. 

Example:

What is the decimal form of 8/32?

Solution:

Step 1: Find the GCF.

The GCF of 8 and 32 is 8.

Step 2: Divide both values by GCF.

8 ÷ 8 = 1 and 32 ÷ 8 = 4

The fraction becomes 1/4.

Step 3: Divide.

1 ÷ 4 is 0.25. So, the decimal form of 8/32 is 0.25. 

The difference between this method and long division is that long division is used for bigger fractions, where finding the GCF manually is difficult. Apart from that, both techniques serve the same purpose.

Making the denominator a power of 10:

This method is difficult and less famous because it requires a lot of mind work. 

Basically, you multiply the numerator and the denominator with such a number that the denominator becomes a power of 10. This method is used on smaller fractions usually. 

Example:

Convert 3/4  into decimal form. 

Solution: 

Step 1: Find the suitable number.

If we multiply 4 by 25, we will get a 100 in the bottom of the fraction. 

Step 2: Multiply with 25.

= (3 x 25) / (4 x 25)

= 75/100

Step 3: Count the 0’s and add the decimal point in the numerator accordingly from the right.

There are 2 zeros in 100. If we count 2 digits in 75, then the decimal point will be placed before 7. Like 0.75. This is the decimal form of 3/4.