Partial Fraction Calculator

Partial Fraction Calculator

Partial Fraction Calculator is used to determine the solution of the complex rational expression into a simple fraction by entering the values in the input box and giving results with detailed steps.

What is a partial fraction?

Partial fraction is used to decompose the rational expression (quotient of two polynomials) from improper fraction to the sum of the simpler fraction. Due to this, it is also known as the partial fraction decomposition and partial fraction expansion method.

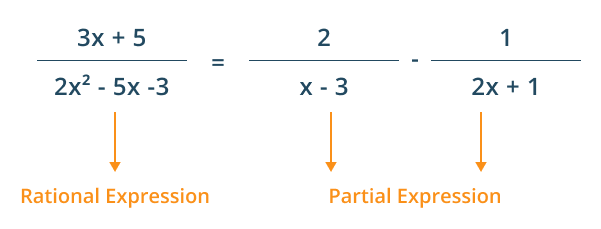
In other words, the process of partial fractions converts the long polynomial into the sum of two or more polynomials in the form of a numerator and denominator. When simplifying the sum of the simple polynomial then get the original long polynomial expression.

In calculus, partial fraction plays an important role in solving the definite integral of rational expression as well as the indefinite integral of the rational expression. The general form of the partial expression can be represented as,

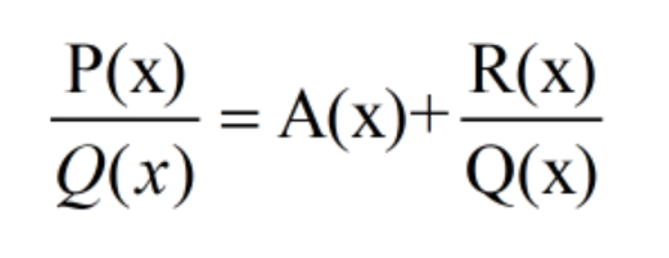
Formulas of partial fraction

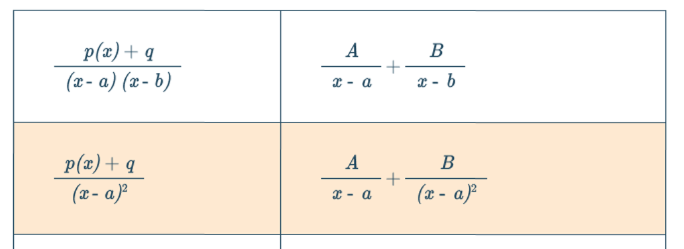
There are different formulas of the partial fraction depending on the degree of the denominator term and the number of polynomial functions in the denominator of the original function.

Types of Partial Fraction

Types of partial fractions are dependent on the degree of the numerator and the denominator. There are two basic types of partial fractions.

• Improper fraction
• Proper fraction

Proper fraction

In this fraction, the degree of the polynomial in the numerator is less than the degree of the polynomial in the denominator. To solve this fraction use the appropriate formula of partial fraction and simplify the terms using an algebraic technique.

Improper fraction

In this fraction, the degree of the polynomial in the numerator is greater than the degree of the polynomial in the denominator. To solve this fraction first reduce improper fraction in the form of a proper fraction using the remainder theorem. Divide the numerator with the denominator to get the resultant in the sum of polynomial/constant and proper fraction.

Steps to solve the rational polynomial expression

Follow the below steps to solve the rational polynomial expression.

• Firstly, make the fraction in proper form if it is given in improper form using the remainder theorem.
• Make the factor of the denominator polynomial of the proper fraction if needed.
• Write each factor of the denominator with a variable say “A, B, & C” in the numerator.
• Solve the fractions to determine the value of unknown variables “A, B, & C” by using LCM method of a fraction.
• Solve the values of the variable using the system of linear equations and compare the coefficient of a degree of “x”.
• Lastly, substitute the values of unknown variables “A, B, & C” in the partial fraction and get the final results.

How to decompose the rational expression in Partial Fraction?

Here, we provide some manual examples to convert rational polynomial expressions into partial fractions.

Example 1

Solve the 6x3 / (x+1)3 fraction.

Solution

Step 1: Given expression is in the form of an improper fraction then first convert it into the proper fraction.

= 6x³/(x+1)³

Open the formula of the denominator and the fraction becomes.

= 6x³/(x³+ 3x²+ 3x +1)

Step 2: Use a long division method to convert it into a proper fraction.

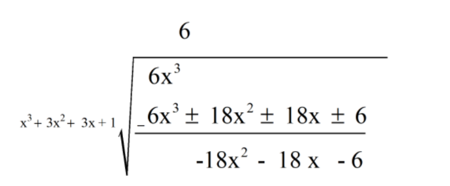
Then, it can be written as,

= 6 + (−18x²−18x−6)/(x+1)³

Step 3: Partial fraction decomposition using unknown variables written as.

(−18x²−18x−6)/(x+1)³= (A)/(x+1)+ (B)/(x+1)² + (C)/(x+1)³       ---------------->(i)

Multiply the denominator on both sides of the above equation.

−18x²−18x−6 = A(x+1)² + B(x+1) + C        ---------------->(ii)

Step 4: By expanding the left side of the eq(ii).

−18x² − 18x − 6= Ax²+ 2Ax + A + B x + B + C         ---------------->(iii)

Step 5: By separating the like variables 

−18x² − 18x – 6 = Ax² + x (2A+B) + A + B + C          ---------------->(iv)

Step 6: By comparing the coefficients of all variables and constants.

2A + B = −18         ---------------->(a)

A = −18         ---------------->(b)

A + B + C = −6         ---------------->(c)

Solving it using a system of linear equations we got the value unknown.

Put the value of “A = -18” in the equation (a).

2(-18) + B = −18                                        

-36 + B = −18   

B = −18 + 36

B = 18

Put the value of “A & B” in the equation (c).

-18 + 18 + C = −6

C = −6

Then, the answer of A, B, & C becomes.

A=−18, B=18, C=−6

Step 7: Now substitute the values of “A, B, & C” in the equation (i) and get the final results.

6x³/(x+1)³= 6+ (−18)/(x+1) + (18)/ (x+1)²+ (−6)/ (x+1)³

6x3/(x+1)3= 6 – 18/(x+1) + 18/(x+1)2 − 6/(x+1)3