To calculate result you have to disable your ad blocker first.
Power Series Calculator
To evaluate the power series of a function with steps, input the function and other values in the given input box and hit calculate button using power series calculator.
Table of Contents:
Power Series Calculator
Find the power series expansion and representation using the power series calculator with steps. It also gives a plot of approximation of x up to certain order.
For a concept as complex as power series, this tool does a fair job of making its calculation easy. You can convert any function into a power series using this calculator. The built-in keyboard aids in the input of special operations.
How to use this calculator?
Follow the given instructions:
- Enter the function. (Take help from the keyboard and examples.)
- Select the variable.
- Input point and order.
- Click Calculate.
Order means the power of the variable till which you want to find the series.
Let’s learn more about the power series, its form, and how to expand and represent functions using power series with examples.
What is a power series?
Power series is a type of series expansion of a function into polynomials with infinite terms. It is used by calculators and other computing devices for the evaluation of functions like exponential, logarithmic e.t.c
Say you have two functions;
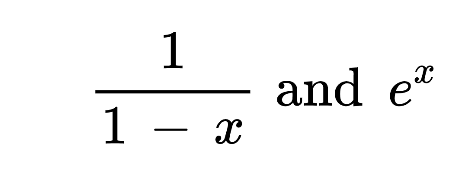
If you wanted to perform any kind of mathematical operation on them like addition or subtraction, How would you do it?
The easiest way is to convert these functions into the polynomial form and then apply the operation. But it cannot be done just like that. There are some rules.
This is where the power series is used. On expanding these functions using the power series formula, they look like this.
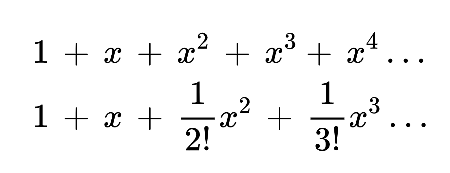
Note: The (!) is factorial.
It is now very easy to add, subtract, or divide these values.
Power series are used in limits and approximate evaluation of integrals. Another important use of power series is error estimation.
Form of power series:
Also known as the formula of power series or its syntax, It basically tells what a power series looks like.
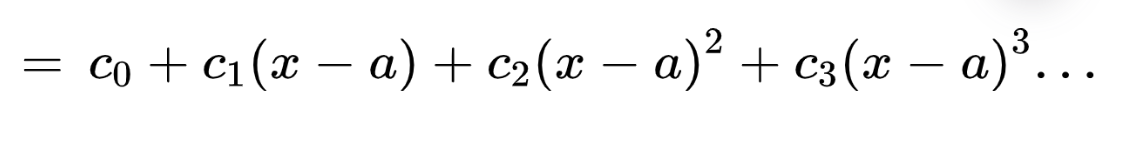
It can be written with the summation sign as well.
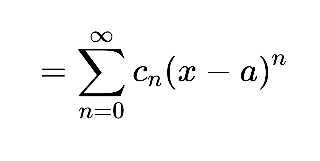
Here:
- c represents constant terms.
- x is the variable of function f(x).
- a is called the center.
This term a is subtracted from the variable because in general functions can have different centers. For instance, for a quadratic equation y = x2, the parabolic graph is:
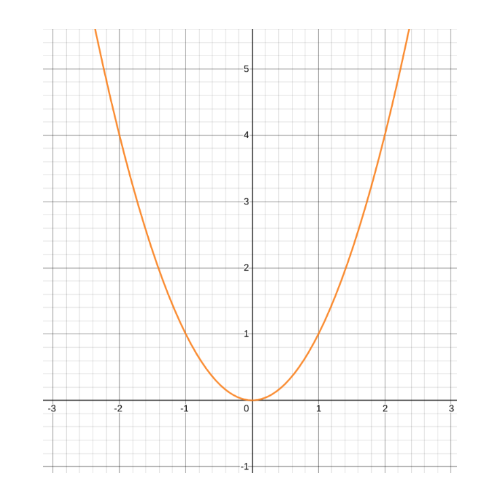
The center is 0. But the function could have a different center. Like in the case of equation y = ( x - 3 )2, the graph is centered at 3.
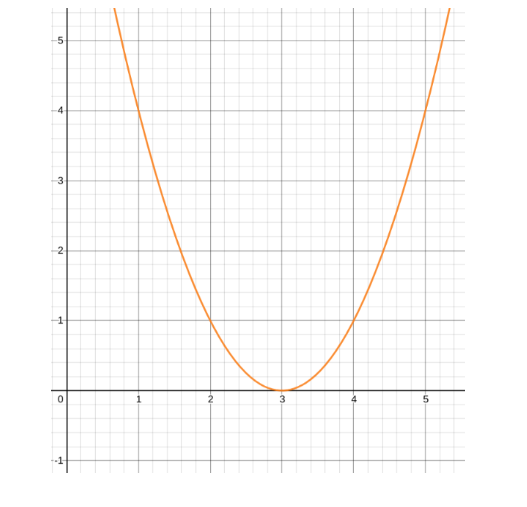
Hence a is used for generalization so that such functions can be included as well.
How to represent functions in power series?
It is convenient to represent a function in the series form before expanding it as it serves as a formula. Remember that the domain of this function should be the interval of convergence.
We basically manipulate the power series representation of an easy and basic function, here the geometric series. It is represented as:
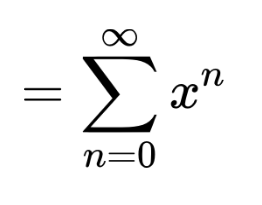
This series converges when the absolute value of x is less than one (i.e |x| < 1) and at this point its value is 1/(1 - x). So,
![]()
This is the power series representation because the domain is an interval of convergence at this certain value.
Now, we can use this value to represent other functions. Such as:
![]()
As long as the absolute value of -x is less than one, it eventually means the same thing as |x|<1.
For a little complex function:
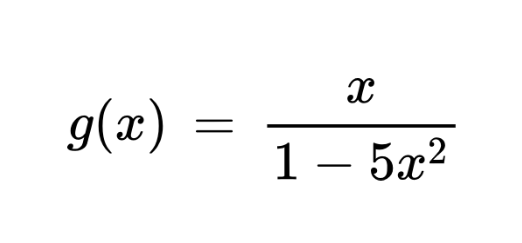
Separate out the x and it is almost already in the required form.
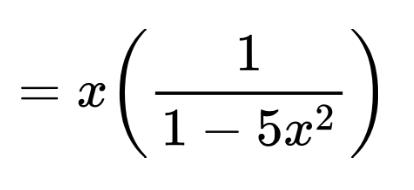
Therefore writing to represent in power series.
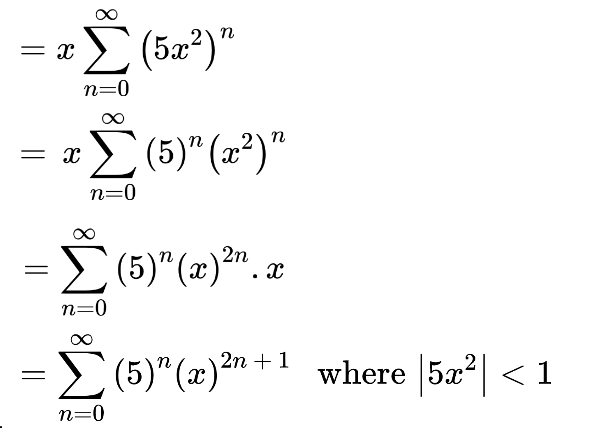
How to expand the power series?
Enter the numbers at the place of n and solve up to the required order. You can use the sum of the power series calculator as an alternative.
Example:
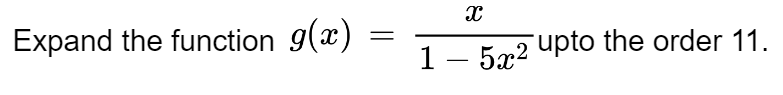
Solution:
Step 1: Data interpretation.
Function = x / (1 - 5x2)
Point = 0
Order = 11
Step 2: Represent in the power series form.
As already done above
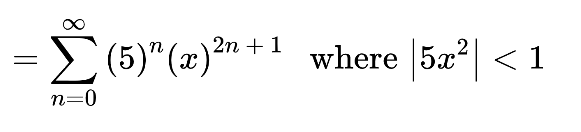
Step 3: Enter the numbers in the expression and solve.
= (5)0(x)2(0) + 1 = (1)(x)0+1 = x
= (5)1(x)2(1) + 1 = (5)(x)2+1 = 5x3
= (5)2(x)2(2) + 1 = (25)(x)4+1 = 25x5
= (5)3(x)2(3) + 1 = (125)(x)6+1 = 125x7
= (5)4(x)2(4) + 1 = (625)(x)8+1 = 625x9
= (5)5(x)2(5) + 1 = (3125)(x)10+1 = 3125x11
(the order 11 is computed at last)
Step 4: Write in the series form.
= x + 5x3 + 25x5 + 125x7 + 625x9 + 3125x11 + 0(x13)