kalkulator integral

Integral Calculator adalah alat online yang menghitung antiderivatif fungsi. Ini berfungsi sebagai kalkulator integral yang pasti serta kalkulator integral yang tidak terbatas dan memungkinkan Anda memecahkan nilai integral dalam waktu singkat.

Kalkulator integrasi baris menunjukkan semua langkah yang diperlukan untuk mengevaluasi integral. Ini melakukan integrasi fungsi dengan bagian-bagian dan memecahkan integral dengan dua metode yang berbeda.

Apa itu integral?

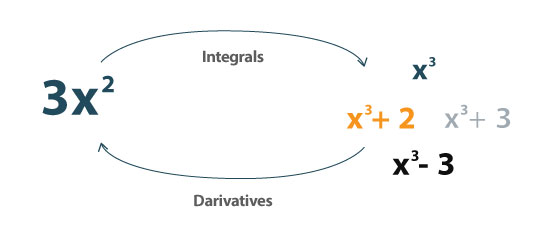
Sebuah integral adalah kebalikan dari turunannya. Ini dapat digunakan untuk menentukan area di bawah kurva.

Ini dapat didefinisikan sebagai:

"Integral memberikan nomor pada fungsi dengan cara yang dapat menggambarkan perpindahan, area, volume, dan konsep-konsep lain yang muncul dengan menggabungkan data infinesimal. Integrasi adalah salah satu dari dua operasi utama kalkulus; Operasi terbaliknya adalah diferensiasi (mengambil derivatif). "

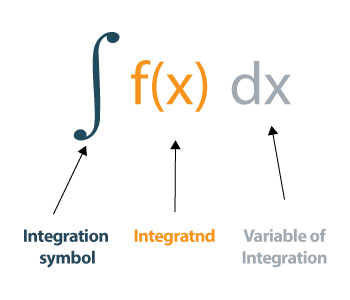
Bagaimana cara mengevaluasi integral?

Anda mungkin ingin tahu bagaimana menyelesaikan integral secara manual. Ini bisa entah bagaimana menjengkelkan bagi orang-orang yang baru memulai dengan integral. Tapi, jangan khawatir. Kami akan menunjukkan perhitungan dengan contoh-contoh sehingga Anda dapat memahami dengan mudah.

Mari kita gunakan contoh untuk memahami metode untuk menghitung integral online yang pasti. 

Contoh - Integral yang pasti

Untuk fungsi f (x) = x - 1, temukan integral yang pasti jika intervalnya [1, 10].

Larutan:

Langkah 1: Tentukan dan tulis fungsi f (x).

F (x) = x - 1

Interval = [1, 10]

Langkah 2: Ambil antiderivatif fungsi dan tambahkan konstanta.

= ∫ (x−1) dx = (x²/2) – x + C

Langkah 3: Hitung nilai batas atas F (a) dan batas bawah f (b).

Sebagai, a = 1, dan b = 10,

F(a) = F(1) = (1²/2) - 1 = -0.5

F(b) = F(10) = (10²/2) - 10 = 40

Langkah 4: Hitung perbedaan batas atas F (a) dan batas bawah f (b).

F (b) – F (a) = 40 – (-0.5) = 40.5

Anda dapat menggunakan kalkulator integral ganda di atas jika Anda tidak ingin menikmati perhitungan integral.

Contoh - integral dari fungsi trigonometri

Untuk fungsi f (x) = sin (x), temukan integral yang pasti jika intervalnya [0, 2π].

Larutan:

Langkah 1: Tuliskan fungsi.

F (x) = sin (x)

Interval = [0, 2π]

Langkah 2: Ambil antiderivatif fungsi dan tambahkan C. C.

= ∫ sin(x)dx = - cos(x) + C

Langkah 3: Hitung nilai batas atas F (a) dan batas bawah f (b).

Sebagai, a = 0, dan b = 2π,

F (a) = F (0) = cos (0) = 0

F (b) = F (2π) = cos (2π) = 0

Langkah 4: Hitung perbedaan batas atas F (a) dan batas bawah f (b).

F (b) – F (a) = 0 – 0 = 0

Gunakan pemecah integral di atas untuk memecahkan integral trigonometri dalam sepersekian detik.