To calculate result you have to disable your ad blocker first.
ggT rechner
Geben Sie bis zu 10 Zahlen ein berechnen Sie den größter gemeinsamer teiler (ggT rechner).
Table of Contents:
Der ggT Rechner ist ein effizienter ggT-Finder , der den größten (höchsten) gemeinsamen Faktor der angegebenen Zahlen berechnet, indem er:
- Liste der Faktoren Methode
- Primfaktorisierungsmethode
- Teilungsmethode
- Euklidischer Algorithmus
- Binärer (Stein's) Algorithmus
- Upside Down Division
Neben ggT (größter gemeinsamer Teiler) wird auch das kleinstes gemeinsames Vielfaches (KGV) für die angegebenen Zahlen berechnet.
In den nächsten Abschnitten werden die vom GCD Rechner verwendeten Methoden zum Ermitteln des ggT, der ggT-Definition, zum Berechnen des ggT ohne Verwendung des ggT-Rechners sowie einige Beispiele zum Ermitteln des größten gemeinsamen Faktors erläutert.
Was ist ggT?
Der größte gemeinsame Faktor (ggT) einer Reihe von Zahlen ist der größte Faktor, den alle Zahlen gemeinsam haben. Es ist allgemein als der höchste gemeinsame Faktor (ggT) bekannt.
Zum Beispiel haben 8, 12 und 16 zwei gemeinsame Faktoren, nämlich 2 und 4. Der größte ist 4. Der ggT von 8, 12 und 16 ist also 4.

Wie berechnet man den ggT?
Wenn Sie bereits hier sind, möchten Sie vielleicht wissen, wie Sie den ggT finden . GgT kann mit verschiedenen Methoden berechnet werden. Im Folgenden finden Sie verschiedene Methoden zur Berechnung des ggT.
- Faktorisierungsmethode
Beispiel: Ermitteln Sie den ggT von 12 und 16 mithilfe der Faktorisierungsmethode.
Lösung:
Die Methode der Faktorisierung oder Liste der Faktoren verwendet die Faktoren der angegebenen Zahlen, um den höchsten gemeinsamen Faktor zu finden.
Schritt 1: Listen Sie alle Faktoren der angegebenen Zahlen auf.
Schritt 2: Suchen Sie nach dem höchsten gemeinsamen Faktor.

Weitere Informationen finden Sie in der Abbildung unten.
- Teilungsmethode
Beispiel: Ermitteln Sie den ggT von 30 und 42 mithilfe der Teilungsschrittmethode .
Lösung:
Schritt 1: Teilen Sie die größte Zahl durch die kleinste Zahl.
Schritt 2: Nehmen Sie den Divisor aus dem vorherigen Schritt und teilen Sie ihn mit dem Rest, den Sie im vorherigen Schritt erhalten haben.
Schritt 3: Wiederholen der 2 nd Schritt , bis der Rest Null wird. Der letzte Teiler ist der höchste (größte) gemeinsame Faktor.
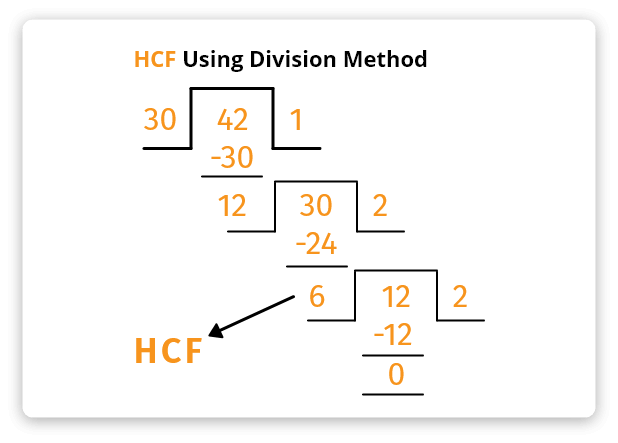
Verwenden Sie den obigen ggT Finder, um das Ergebnis Ihrer manuellen Berechnungen zu überprüfen. In der folgenden Abbildung finden Sie eine Darstellung der Teilungsschrittmethode.
- Primfaktorisierung
Beispiel: Finden des ggT von 24 und 36 , die unter Verwendung von Primfaktorenzerlegung Methode .
Lösung:
Schritt 1: Machen Sie die Faktoren der angegebenen Zahlen mit dem Faktorbaum, wie in der Abbildung unten gezeigt.
Schritt 2: Markieren oder umkreisen Sie die gemeinsamen Faktoren der angegebenen Zahlen.
Schritt 3: Multiplizieren Sie alle gängigen Faktoren, um den ggT zu erhalten. Wenn es nur einen gemeinsamen Faktor gibt, muss nicht multipliziert werden.
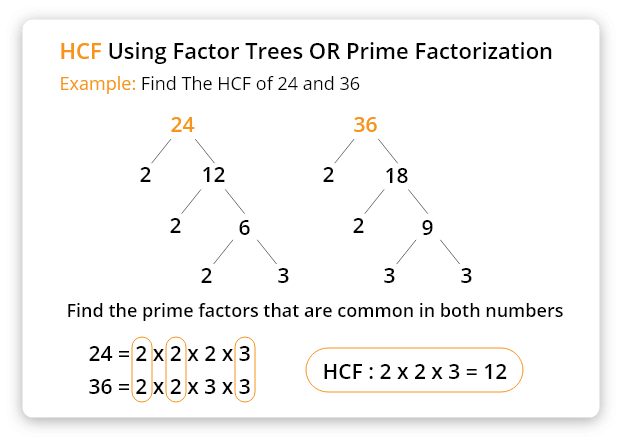
Der größte Rechner für den gemeinsamen Teiler (Nenner) listet alle Schritte der Berechnung auf. Es ist nicht nur ein Berechnungswerkzeug. Es kann auch verwendet werden, um die Methoden zur Berechnung des höchsten gemeinsamen Faktors zu erlernen.
Tabelle des größter gemeinsamer teiler
| ggt von 12 und 16 | 2 |
| ggt von 2 und 5 | 1 |
| ggt von 3 und 4 | 1 |
| ggt von 5 und 25 | 5 |
| ggt von 4 und 5 | 1 |
| ggt von 16 und 24 | 8 |
| ggt von 5 und 7 | 1 |
| ggt von 15 und 20 | 20 |
| ggt von 8 und 12 | 4 |
| ggt von 8,9 und 25 | 1 |
| ggt von 2 und 3 | 1 |
| ggt von 4 und 8 | 4 |
| ggt von 3,4 und 6 | 1 |
| ggt von 3 und 5 | 1 |
| ggt von 680,510 und 340 | 4 |
| ggt von 2 und 8 | 2 |
| ggt von 18 und 48 | 6 |
| ggt von 12 und 48 | 12 |
| ggt von 30 und 42 | 6 |
