To calculate result you have to disable your ad blocker first.
калькулятор пределов
Введите функцию и другие значения в указанные поля ввода. Нажмите кнопку «Рассчитать», чтобы оценить лимит с помощью калькулятора лимитов.
Table of Contents:
Калькулятор пределов используется для оценки предельных функций по указанной переменной. Переменная может быть x, y или z. Предел калькулятор решает границы с шагами и показывает каждую фазу расчета.
Ниже вы найдете определение лимитов, как рассчитать лимиты без использования поиска лимитов, формулу лимитов и некоторые примеры для понимания лимитов.
Какие есть ограничения?
Идея предела функции жизненно важна для изучения исчисления. Он используется при описании некоторых важных теорий в исчислении, таких как определенный интеграл функции, производная функции и непрерывность.
Предел некоторой функция F (X) определяет поведение функции вблизи конкретной й значение. По сути, он не дает значения функции в точке x.
limx→c f(x)= L−−
Предел решателя выше , можно оценить как правый и пределы слева.
Формулы пределов - правила пределов
Ниже мы представили законы пределов.
Обозначение лимита
limx→c f(x)= L−−
Левый предел
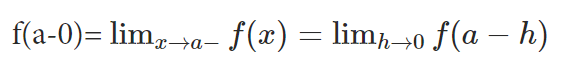
Правый предел
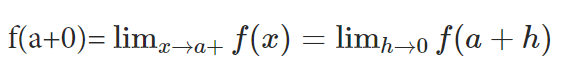
Пределы тригонометрических функций
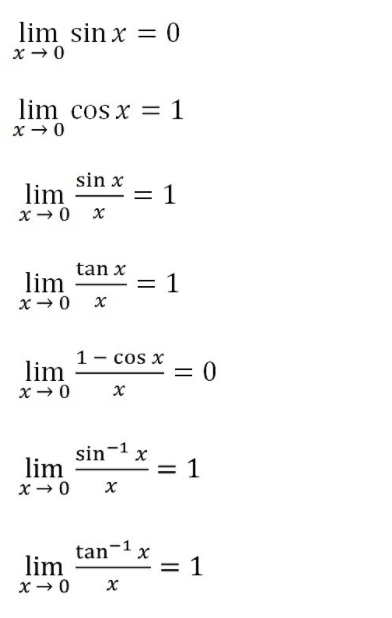
Пределы журналов и экспоненциальных функций
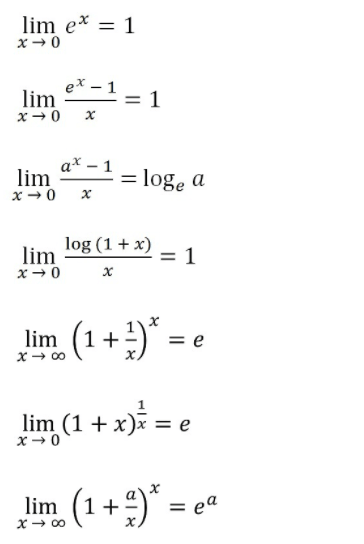
Пределы вида 1 ∞
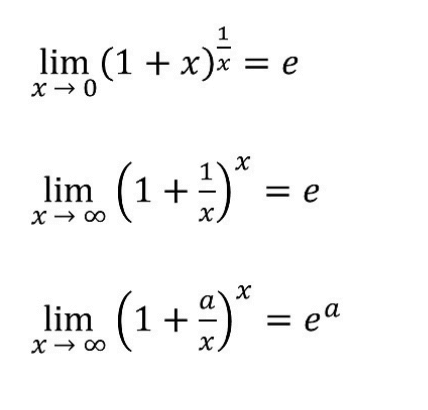
Пределы x^n
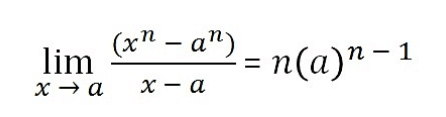
Проверка наличия лимита
Чтобы проверить, существует ли предел для f (x) при x = a, мы проверяем,
Предел слева = Предел справа = f ( a)
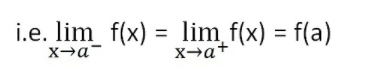
Правило L'hospital
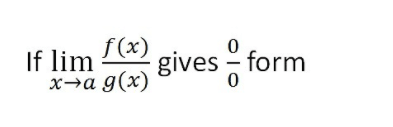
Где,
f ( а) = 0
г ( а) = 0
Потом,
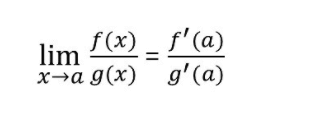
Правило суммы пределов
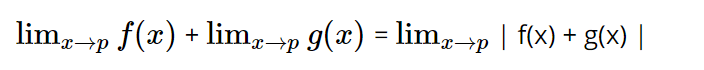
Ограничивает правило продукта
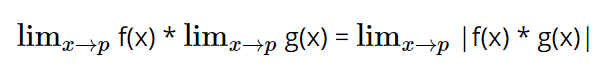
Правило предельного частного
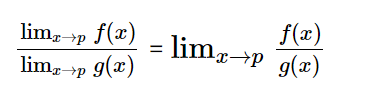
Правило ограничения власти
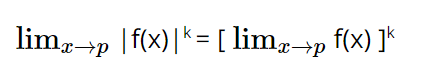
Постоянное правило ограничений
Предел постоянной функции равен постоянной.
Как оценить лимиты?
Оценщик пределов разработан специально для оценки пределов. Но мы объясним ручной метод оценки пределов. Пример ниже иллюстрирует метод из справочника с пошаговыми инструкциями.
Пример :
Evluate :
limx→c f(x)= L−−
Решение:
Шаг 1: Запишите значение.
limx→2 (x3+2x2−5x+2)
Шаг 2: Примените функцию ограничения к каждому элементу.
limx→2 (x3+2x2−5x+2)
Шаг 3: Выведите коэффициенты из предельной функции.
limx→2(x3)+ limx→2(2x2)− limx→2(5x) + limx→2(2)−−
Шаг 4: Примените ограничение, поместив в уравнение x -> 2 . = 1 (2 ^ 3 ) + 2 (2 ^ 2) -5 (2) +2
= 8 + 8-10 + 2
= 8
так,
1 limx→2(x3)+ 2 limx→2(x2)− 5 limx→2(x)+ limx→2(x)+ 2−−
Вы можете использовать приведенный выше калькулятор правил l'hopital, чтобы проверить ответ любой функции ограничения.
Вот график, построенный для указанной выше функции.